A P. 4895. feladat (2017. január)

P. 4895. Egy $\displaystyle \ell$ hosszúságú, $\displaystyle M$ tömegű és egy $\displaystyle 2\ell$ hosszúságú, $\displaystyle 2M$ tömegű homogén rúd az ábra szerinti helyzetben található. Milyen irányú és mekkora gravitációs erő hat az $\displaystyle m$ tömegű pontszerű testre? (Keressünk elemi megoldást!)

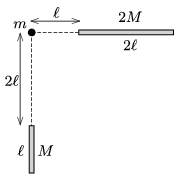
Közli: Kobzos Ferenc, Dunaújváros

(5 pont)

A beküldési határidő 2017. február 10-én LEJÁRT.

Megoldás. Számítsuk ki először a felső (az ábrán vízszintes helyzetű) rúd által az $\displaystyle m$ tömegű testre kifejtett $\displaystyle F_1$ erőt. Mivel a rúd mérete és a testek távolsága összemérhető, az erő nem számolható a pontszerű testek között ható Newton-féle gravitációs vonzóerő képlete alapján. Az sem igaz, hogy a rúd által kifejtett erő akkora lenne, mintha a rúd teljes tömege a rúd tömegközéppontjában helyezkedne el. (Ez csak gömbszimmetrikus tömegeloszlások esetében lenne igaz.) A vonzóerőt a rúd kicsiny darabkákra osztásával és az erők összegzésével (integrálásával) nyilván ki lehet számítani, de van egyszerűbb, elemi módszer is.

Tudjuk, hogy két pontszerű test közötti gravitációs potenciális energia

$\displaystyle E=-\gamma\frac{m_1m_2}{r},$

ahol $\displaystyle m_1$ és $\displaystyle m_2$ a testek tömege, $\displaystyle r$ pedig a távolságuk. Távolítsuk el – gondolatban – a $\displaystyle 2M$ tömegű rudat az $\displaystyle m$ tömegű testtől egy kicsiny ($\displaystyle 2L$-nél sokkal kisebb) $\displaystyle \Delta x$ távolsággal. Ha a rúd és a pontszerű test között ható erő $\displaystyle F_1$, akkor az eltávolítás során

$\displaystyle W=F_1\Delta x$

munkát kell végezzünk, ami a gravitációs helyzeti energia megváltozásával egyenlő. Az energiaváltozás szempontjából csak annyi történt, mintha a rúd egy kicsiny $\displaystyle \Delta x$ hosszúságú, tehát $\displaystyle \Delta m=(M/\ell)\Delta x$ tömegű darabkáját a rúd egyik végétől a másik végére helyeztük volna át, tehát

$\displaystyle F_1\Delta x=\gamma m\frac{M}{\ell}\Delta x \left(-\frac{1}{3\ell}+\frac{1}{\ell}\right),$

vagyis

$\displaystyle F_1=\gamma\frac{mM}{\ell^2}\cdot \frac{2}{3}.$

Hasonló megfontolásokkal adódik, hogy a másik rúd által kifejtett erő

$\displaystyle F_2=\gamma\frac{mM}{\ell^2}\cdot \frac16.$

Ezek szerint az eredő gravitációs erő iránya a hosszabb rúd felé mutató egyenessel

$\displaystyle \alpha=\arctg\frac14\approx 14^\circ-\text{os}$

szöget zár be, és az eredő erő nagysága

$\displaystyle F=\sqrt{F_1^2+F_2^2}=\gamma\frac{\sqrt{17}mM}{6\ell^2}.$

Statisztika:

46 dolgozat érkezett.
5 pontot kapott:	Bekes Nándor, Di Giovanni András, Faisal Fahad AlSallom, Fajszi Bulcsú, Fehér 169 Szilveszter, Ghada Alshalan, Jakus Balázs István, Kondákor Márk, Markó Gábor, Marozsák Tóbiás , Molnár Mátyás, Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Papp 121 Krisztina, Sal Dávid, Tófalusi Ádám, Varga-Umbrich Eszter, Zöllner András.
4 pontot kapott:	Bartók Imre, Elek Péter, Németh Csaba Tibor, Osváth Botond, Pataki 245 Attila, Szentivánszki Soma .
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	8 versenyző.

A KöMaL 2017. januári fizika feladatai