 |
A P. 4899. feladat (2017. január) |
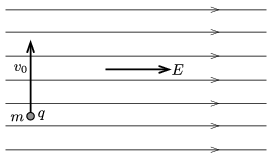
P. 4899. Nagy kiterjedésű, homogén elektromos mező erővonalai vízszintesek. A térerősség nagysága \(\displaystyle E=10^4\) N/C. Ennek a mezőnek egy pontjából \(\displaystyle v_0=2\) m/s függőleges sebességgel feldobunk egy \(\displaystyle m=4\) g tömegű fémgolyót, amelynek előzetesen \(\displaystyle q=3\cdot10^{-6}\) C pozitív töltést adtunk.
\(\displaystyle a)\) Mekkora elmozdulás után lesz a sebességének nagysága a kezdősebességével egyenlő?
\(\displaystyle b)\) Mennyi idő telik el eddig?
\(\displaystyle c)\) Mozgása során mekkora a legkisebb sebessége?
\(\displaystyle d)\) Hol mozog a leglassabban?
Közli: Holics László, Budapest
(4 pont)
A beküldési határidő 2017. február 10-én LEJÁRT.
I. megoldás. Vegyük fel a koordináta-rendszer \(\displaystyle x\) tengelyét vízszintesen (jobbra), az \(\displaystyle y\) tengelyt pedig függőlegesen (felfelé). A fémgolyó \(\displaystyle x\) irányú gyorsulása
\(\displaystyle a_x\equiv \frac{qE}{m}=7{,}5~\frac{\rm m}{\rm s^2},\)
függőleges irányban pedig
\(\displaystyle a_y =-g =-9{,}81~\frac{\rm m}{\rm s^2}.\)
A test elmozdulása \(\displaystyle t\) idő alatt:
\(\displaystyle x(t)=\frac{a}{2}t^2,\qquad y(t)=v_0t-\frac{g}{2}t^2,\)
a sebességkomponensek pedig
\(\displaystyle v_x=at,\qquad v_y=v_0-gt.\)
\(\displaystyle b)\) A sebesség nagysága akkor egyezik meg a kezdősebességgel, ha
\(\displaystyle v_x^2+v_y^2=v_0^2,\)
vagyis
\(\displaystyle (at)^2+\left(v_0-gt\right)^2=v_0^2,\)
azaz az indulástól számítva az eltelt idő
\(\displaystyle t=\frac{2v_0g}{a^2+g^2}\approx 0{,}26~\rm s.\)
\(\displaystyle a)\) A fentebb kapott idő alatt a test elmozdulásvektorának koordinátái:
\(\displaystyle x(t)=\frac{a}{2}t^2\approx 25~{\rm cm},\)
\(\displaystyle y(t)=v_0t-\frac{g}{2}t^2\approx 19~{\rm cm},\)
az elmozdulás hossza pedig
\(\displaystyle \sqrt{25^2+19^2}~{\rm cm}=31~{\rm cm}.\)
\(\displaystyle c)\) A sebesség nagyságának négyzete \(\displaystyle t\) idejű mozgás után
\(\displaystyle \vert \boldsymbol v\vert^2=v_x^2+v_y^2=(a^2+g^2)t^2-2v_0gt+v_0^2.\)
Ez a kifejezés \(\displaystyle t\) másodfokú függvénye, amelynek minimumát pl. teljes négyzetté alakítással, esetleg deriválással határozhatjuk meg, vagy úgy, hogy megkeressük a grafikonjának (egy parabolának) a szimmetriatengelyét. Az eredmény:
\(\displaystyle t_0=\frac{v_0g}{a^2+g^2}\approx 0{,}13~\rm s.\)
(Megjegyzés: \(\displaystyle t_0\) a \(\displaystyle b)\) kérdésben szereplő időtartamnak éppen a fele.) Ezen időpontban a sebesség nagysága (ami a sebesség nagyságának minimuma):
\(\displaystyle v_\text{min}=\sqrt{v_x^2+v_y^2}\approx 1{,}2~\frac{\rm m}{\rm s}.\)
\(\displaystyle d)\) A fémgolyó mozgása \(\displaystyle t=t_0\) időpontban a leglassabb, ekkor a helyének koordinátái:
\(\displaystyle x(t_0)=6{,}3~{\rm cm}\qquad \text{és}\qquad y(t_0)=17{,}7~{\rm cm}.\)
Ez a pont a feldobás helyétől 18,8 cm távol van.
II. megoldás. A fémgolyó homogén (elektromos + gravitációs) erőtérben mozog, emiatt a gyorsulása állandó. A gyorsulás vektora
\(\displaystyle g'= \sqrt{ g^2+a^2 }=12{,}3~\frac{\rm m}{\rm s^2}\)
nagyságú, és az irányának a függőlegessel bezárt szöge
\(\displaystyle \alpha=\arctg\frac{a}{g}=37{,}3^\circ.\)
A golyó mozgása egy elforgatott koordináta-rendszerben \(\displaystyle g'\) nehézségi gyorsulású ,,gravitációs'' erőtérben végbemenő, \(\displaystyle v_0\) nagyságú és \(\displaystyle \alpha\) hajlásszögű kezdősebességgel induló ferde hajításként is tárgyalható. Az így kapott eredmények (ha azokat ,,visszaforgatjuk'' az eredeti koordináta-rendszerbe) megegyeznek az I. megoldás eredményeivel.
Statisztika:
75 dolgozat érkezett. 4 pontot kapott: Balaskó Dominik, Balog 518 Lóránd, Bartók Imre, Bekes Nándor, Csuha Boglárka, Debreczeni Tibor, Édes Lili, Fajszi Bulcsú, Fazakas Réka, Fehér 169 Szilveszter, Fekete Balázs Attila, Gál Péter Levente, Guba Zoltán, Horváth 122 Aurél, Illés Gergely, Illyés András, Jánosik Áron, Keltai Dóra, Kolontári Péter, Kormányos Hanna Rebeka, Krasznai Anna, Magyar Róbert Attila, Makovsky Mihály, Markó Gábor, Marozsák Tóbiás , Nagy 284 Domonkos, Nagy 555 Botond, Olosz Adél, Páhoki Tamás, Papp 121 Krisztina, Pataki 245 Attila, Paulovics Péter, Póta Balázs, Sal Dávid, Sugár Soma, Szentivánszki Soma , Tibay Álmos, Tóth 111 Máté , Varga-Umbrich Eszter, Weisz Máté, Zöllner András, Zsombó István. 3 pontot kapott: 13 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 8 versenyző.
A KöMaL 2017. januári fizika feladatai
