A P. 4919. feladat (2017. március)

P. 4919. Egy \(\displaystyle m_1\) tömegű kiskocsit az ábrán látható módon egy bizonyos magasságban elhelyezett, vízszintes, merev sínpárra helyeztünk. A kocsi aljához erősített (a sínek között lelógó) fonál végén egy \(\displaystyle m_2\) tömegű kicsiny golyó található. (A fonál hossza lényegesen nagyobb, mint a kiskocsi és a golyó mérete.)

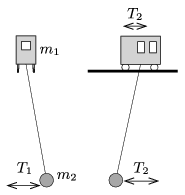
Ha a golyót a sínekre merőleges irányban kissé kitérítjük a stabil egyensúlyi helyzetéből, a kialakuló lengés periódusideje \(\displaystyle T_1\). Ha a kiskocsi rögzített helyzetében a golyót a sínekkel párhuzamosan térítjük ki egy kicsit, majd mindkét testet elengedjük, a rezgés periódusideje \(\displaystyle T_2\). Mekkora az \(\displaystyle m_2/m_1\) arány, ha \(\displaystyle T_1/T_2=2\)? (A súrlódás és a légellenállás elhanyagolható.)

Közli: Szász Krisztián, Budapest

(5 pont)

A beküldési határidő 2017. április 10-én LEJÁRT.

Megoldás. A sínekre merőlegesen kitérített golyó (mint matematikai inga)

\(\displaystyle T_1=2\pi\sqrt{\frac{\ell}{g}}\)

lengésidővel mozog.

A sínekkel (jó közelítéssel) párhuzamos mozgás során a kiskocsi és a golyó tömegközéppontja vízszintes irányban nem mozdul el, a függőleges elmozdulása pedig (kis kitérések esetén) másodrendűen kicsi, elhanyagolható. A fonalat feszítő erő \(\displaystyle m_2g\), hiszen a golyó függőleges irányú elmozdulása (és így a gyorsulása is) elhanyagolhatóan kicsi. Ha a kiskocsi elmozdulása \(\displaystyle x\), a sínek alatt \(\displaystyle h=\ell\frac{m_2}{m_1+m_2}\) mélyen lévő tömegközépponton áthaladó fonál a kiskocsira

\(\displaystyle F=-m_2g\frac{x}{h}=-\left(m_1+m_2\right) \frac{g}{\ell}\, x\)

vízszintes irányú erőt fejt ki, ami a harmonikus rezgőmozgást végző test mozgásegyenlete szerint \(\displaystyle -m_1x\omega_2^2\)-tel egyenlő. Innen következik, hogy a lengésidő ebben az esetben

\(\displaystyle T_2=\frac{2\pi}{\omega_2}=2\pi \sqrt{\frac{\ell}{g}\, \frac{m_1}{m_1+m_2}}=T_1\sqrt{\frac{m_1}{m_1+m_2}}.\)

(Ugyanezt az eredményt kapjuk, ha a golyó vízszintes irányú mozgásegyenletét írjuk fel.)

A megadott \(\displaystyle T_1/T_2=2\) feltétel akkor teljesül, ha \(\displaystyle m_2/m_1=3.\)

Statisztika:

32 dolgozat érkezett.
5 pontot kapott:	Bartók Imre, Bekes Nándor, Csire Roland, Csuha Boglárka, Debreczeni Tibor, Di Giovanni András, Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Jánosik Áron, Krasznai Anna, Markó Gábor, Marozsák Tóbiás , Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Ónodi Gergely, Páhoki Tamás, Póta Balázs, Sal Dávid, Szentivánszki Soma , Tófalusi Ádám, Varga-Umbrich Eszter, Zöllner András.
4 pontot kapott:	Papp 121 Krisztina.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2017. márciusi fizika feladatai