A P. 4930. feladat (2017. április)

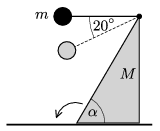
P. 4930. Vízszintes, elég érdes talajon egy derékszögű háromszög keresztmetszetű, \(\displaystyle M\) tömegű, homogén anyageloszlású hasáb fekszik a legkisebb oldallapján. A háromszögnek a talajnál lévő csúcsához tartozó hegyesszöge \(\displaystyle \alpha=60^\circ\). A hasáb felső élének közepéhez egy fonalat erősítettünk, és annak másik végéhez egy \(\displaystyle m\) tömegű, kicsiny testet rögzítettünk. A fonálingát az ábrán látható módon vízszintes helyzetbe hozzuk, majd elengedjük. Azt tapasztaljuk, hogy amikor a fonál \(\displaystyle 20^\circ\)-os szöget zár be a vízszintessel, a hasáb megbillen.

\(\displaystyle a)\) Mekkora a \(\displaystyle M/m\) tömegarány?

\(\displaystyle b)\) Mekkorára kellene növelni a \(\displaystyle M/m\) arányt, hogy a mozgó fonálinga egyáltalán ne tudja megbillenteni a hasábot?

Közli: Berke Martin, Zalaegerszeg, Zrínyi M. Gimn.

(5 pont)

A beküldési határidő 2017. május 10-én LEJÁRT.

Megoldás. Jelöljük a fonál hosszát \(\displaystyle \ell\)-lel, a háromszög átfogóját pedig \(\displaystyle L\)-lel. Amikor a fonál \(\displaystyle \varphi\) szöget zár be a vízszintessel, az inga nehezékének sebessége az energiamegmaradás

\(\displaystyle \frac{1}{2}mv^2=mg\ell\sin\varphi\)

tétele szerint

\(\displaystyle v= \sqrt{2g\ell\sin\varphi}.\)

A fonalat feszítő \(\displaystyle K\) erő a fonál irányú mozgásegyenletből számítható ki:

\(\displaystyle K-mg\sin\varphi=m\frac{v^2}{\ell},\qquad \text{ahonnan} \qquad K=3mg\sin\varphi.\)

Ez a fonálerő, amely

\(\displaystyle K_1=K\cos\varphi= 3mg\sin\varphi\cos\varphi\)

nagyságú vízszintes és

\(\displaystyle K_2=K\sin\varphi= 3mg\sin^2\varphi\)

nagyságú függőleges komponensre bontható, forgatónyomatékot fejt ki a hasáb alsó (bal oldali) oldaléle körül. Ugyancsak van forgatónyomatéka ezen él körül a hasábra ható \(\displaystyle Mg\) nagyságú nehézségi erőnek is. Az eredő forgatónyomaték:

\(\displaystyle f(\varphi)=K_1\cdot L\sin\alpha-K_2\cdot L\cos\alpha- Mg\cdot \frac{2L}{3}\cos\alpha=\)

\(\displaystyle a)\) Kezdetben (az inga elindulásakor) a fenti forgatónyomaték negatív (az óramutató járásával megegyező irányú), majd fokozatosan csökken a nagysága és a megadott \(\displaystyle \varphi=20^\circ\)-nál nullává válik, majd előjelet vált. Ennél a fonálhelyzetnél billen meg a hasáb. A fenti zárójeles kifejezés eltűnéséből a kérdéses tömegarányra az

\(\displaystyle \frac{M}{m}=\frac{9}{2\cos 60^\circ}\left(\sin 20^\circ \cos 20^\circ \sin 60^\circ-\sin^2 20^\circ\cos60^\circ\right)\approx 2{,}0 \)

eredményt kapjuk.

\(\displaystyle b)\) A hasáb megbillenésének feltétele az (1) egyenlet zárójeles kifejezésének eltűnése:

\(\displaystyle \frac{2M}{9m}\cos\alpha=\sin\varphi\cos\varphi\cdot \sin\alpha-\sin^2\varphi\cdot \cos\alpha= \frac{\sin(2\varphi)}{2}\sin\alpha-\frac{1-\cos(2\varphi)}{2}\cos\alpha,\)

amit ilyen alakban is írhatunk:

Ha

\(\displaystyle \frac Mm >\frac94\left(\frac{1}{\cos\alpha}-1\right)=2{,}25,\)

akkor (2) jobb oldala 1-nél nagyobb, az egyenlet nem teljesülhet, tehát a hasáb nem billenhet meg. Az \(\displaystyle M=2{,}25\,m\) határesetben a forgatónyomaték \(\displaystyle \varphi=\tfrac12\alpha=30^\circ\)-nál ugyan nullává válik, de nem vált előjelet, tehát a hasáb ilyen tömegarány esetén sem billen fel.

Statisztika:

45 dolgozat érkezett.
5 pontot kapott:	Bartók Imre, Bekes Nándor, Bukor Benedek, Csire Roland, Csuha Boglárka, Debreczeni Tibor, Édes Lili, Guba Zoltán, Jakus Balázs István, Kavas Katalin, Klučka Vivien, Kozák András, Krasznai Anna, Magyar Róbert Attila, Mamuzsics Gergő Bence, Marozsák Tóbiás , Molnár Mátyás, Morvai Orsolya, Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Paulovics Péter, Póta Balázs, Pszota Máté, Sal Dávid, Szentivánszki Soma , Tófalusi Ádám, Tóth Máté, Weisz Máté.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	6 versenyző.

A KöMaL 2017. áprilisi fizika feladatai