A P. 5009. feladat (2018. február)

P. 5009. Vákuumban \(\displaystyle B=2\) T indukciójú homogén, vízszintes irányú mágneses térben \(\displaystyle \ell=0{,}8\) m hosszú, igen vékony fonalú ingát a \(\displaystyle \boldsymbol B\)-re merőleges síkban vízszintesen kitérítünk, majd kezdősebesség nélkül elengedünk az ábra szerint.

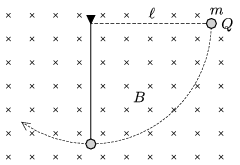
\(\displaystyle a)\) Mekkora töltést kell adnunk az inga \(\displaystyle m=0{,}1\) g tömegű gömbjének, hogy a legalsó ponton áthaladva a fonálerő a mágneses tér nélküli értékének 99%-a legyen?

\(\displaystyle b)\) Mekkora az egymás utáni két áthaladáskor mérhető fonálerők aránya?

Közli: Holics László, Budapest

(4 pont)

A beküldési határidő 2018. március 12-én LEJÁRT.

Megoldás. \(\displaystyle a)\) A mágneses mező nem végez munkát, így az inga gömbje

\(\displaystyle v=\sqrt{2g\ell}=3{,}96~\frac{\rm m}{\rm s}\approx 4~\frac{\rm m}{\rm s}\)

sebességgel halad át a pályájának legalsó pontján. A test gyorsulása ekkor

\(\displaystyle a=\frac{v^2}{\ell}=2g\)

függőlegesen felfelé, és a rá ható Lorentz-erő \(\displaystyle QvB\) (\(\displaystyle Q>0\) esetén) függőlegesen lefelé. Ha a fonalat feszítő erő \(\displaystyle K\), a mozgásegyenlet:

\(\displaystyle mg+QvB-K=-2mg,\)

ahonnan

\(\displaystyle K=3mg+QvB.\)

Mágneses tér nélkül a fonálerő \(\displaystyle 3mg\) lenne, így a megadott feltétel akkor teljesül, ha

\(\displaystyle Q=-0{,}01 \frac{3mg}{B\sqrt{2g\ell}}\approx -3{,}7\cdot 10^{-6}~\rm C.\)

\(\displaystyle b)\) Amikor a töltött test ellenkező irányban halad át a legmélyebb ponton, a Lorentz-erő növeli a fonálerőt, annak értéke

\(\displaystyle K'=3mg-QvB=1{,}01\cdot 3mg\)

lesz. A kétféle irányú sebességhez tartozó erők aránya

\(\displaystyle \frac{K'}{K}=\frac{1{,}01}{0{,}99}=1{,}02.\)

Statisztika:

52 dolgozat érkezett.
4 pontot kapott:	Balaskó Dominik, Bálint Ádám, Bartók Imre, Békési Ábel, Berke Martin, Bukor Benedek, Conrád Márk, Csire Roland, Édes Lili, Guba Zoltán, Háder Márk István, Hajnal Dániel Konrád, Illés Gergely, Klučka Vivien, Kolontári Péter, Kondákor Márk, Kovács Gergely Balázs, Kozák 023 Áron, Kozák András, Magyar Róbert Attila, Makovsky Mihály, Mamuzsics Gergő Bence, Marozsák Tóbiás , Máth Benedek, Molnár Mátyás, Németh Csaba Tibor, Olosz Adél, Póta Balázs, Pszota Máté, Sal Dávid, Surján Botond, Szakály Marcell, Tafferner Zoltán.
3 pontot kapott:	Bíró Dániel, Bonifert Balázs, Boros Máté, Csuha Boglárka, Debreczeni Tibor, Fajszi Bulcsú, Fekete Balázs Attila, Gál Péter Levente, Jánosik Áron, Kántor Bence, Lipták Gergő, Pálfi Fanni, Richlik Róbert, Schrott Márton, Takács Árpád, Turcsányi Máté.
2 pontot kapott:	3 versenyző.

A KöMaL 2018. februári fizika feladatai