 |
A P. 5024. feladat (2018. április) |
P. 5024. Egy \(\displaystyle m\) tömegű testet \(\displaystyle D\) direkciós erejű, feszítetlen állapotában \(\displaystyle \ell\) hosszúságú gumiszálra függesztünk. Ezután az egyensúlyban lévő testet lassan húzzuk úgy, hogy az mindig a test kezdeti helyzetéhez tartozó vízszintes egyenesen mozogjon. Mekkora lesz a kitérítő erő nagysága, amikor a gumiszál a függőlegessel \(\displaystyle \varphi\) szöget zár be?
Adatok: \(\displaystyle \ell=0{,}5\) m, \(\displaystyle \varphi=30^\circ\), \(\displaystyle m=0{,}4\) kg, \(\displaystyle D=10\) N/m.
Közli: Wiedemann László, Budapest
(4 pont)
A beküldési határidő 2018. május 10-én LEJÁRT.
Megoldás. Ha a testet nem húzzuk, a nehézségi erő és a gumiszál rugalmas ereje tart egyensúlyt. A gumi megnyúlása ilyenkor \(\displaystyle \Delta\ell=mg/D\).
Ha a gumifonalat \(\displaystyle \varphi\) szöggel kitérítjük vízszintesen, akkor a hossza
\(\displaystyle \ell+\Delta\ell'=\left(\ell+\frac{mg}{D}\right)\frac{1}{\cos\varphi},\)
a megnyúlása
\(\displaystyle \Delta\ell'=\frac{mg}{D}\frac{1}{\cos\varphi}+\ell\left(\frac{1}{\cos\varphi}-1\right),\)
a benne ébredő rugalmas erő pedig
\(\displaystyle F=D\Delta\ell'=\frac{mg}{\cos\varphi}+D\ell\left(\frac{1}{\cos\varphi}-1\right) \)
lesz.
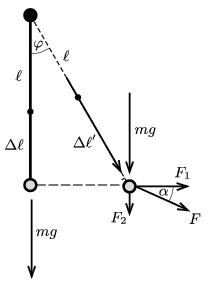
A rugalmas erő és a nehézségi erő eredőjével tart egyensúlyt a külső erő. Ennek vízszintes komponense
\(\displaystyle F_1=F\sin\varphi=\left(mg+D\ell(1-\cos\varphi)\right)\tg\varphi=2{,}65~\rm N,\)
a függőleges komponens pedig
\(\displaystyle F_2=F\cos\varphi-mg=D\ell(1-\cos\varphi)=0{,}67~\rm N.\)
A kitérítő erő nagysága tehát
\(\displaystyle F=\sqrt{F_1^2+F_2^2}=2{,}73~\rm N,\)
iránya pedig \(\displaystyle \alpha=\arctg\frac{F_2}{F_1}=14{,}2^\circ\)-ot zár be a vízszintessel, és ferdén lefelé mutat.
Statisztika:
61 dolgozat érkezett. 4 pontot kapott: Bartók Imre, Békési Ábel, Bíró Dániel, Bukor Benedek, Csécsi Marcell, Csire Roland, Csuha Boglárka, Debreczeni Tibor, Elek Péter, Fekete Balázs Attila, Fialovszky Márk, Garamvölgyi István Attila, Geretovszky Anna, Guba Zoltán, Horváth 999 Anikó, Illés Gergely, Jánosik Áron, Kolontári Péter, Kondákor Márk, Kovács 314 Balázs, Kozák András, Lipták Gergő, Magyar Róbert Attila, Mamuzsics Gergő Bence, Markó Gábor, Máth Benedek, Merkl Gergely, Merkl Levente, Morvai Orsolya, Németh Csaba Tibor, Olosz Adél, Ónodi Gergely, Pácsonyi Péter, Rusvai Miklós, Sal Dávid, Schneider Anna, Schrott Márton, Turcsányi Máté, Urszuly Csenge, Viczián Anna, Vígh Márton. 3 pontot kapott: Bonifert Balázs, Sas 202 Mór. 2 pontot kapott: 13 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2018. áprilisi fizika feladatai
