Problem P. 5083. (December 2018)

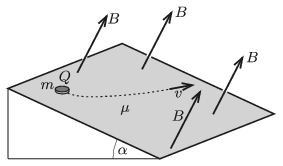
P. 5083. The angle of elevation of a slope is \(\displaystyle \alpha\), the coefficient of friction on its surface is \(\displaystyle \mu\). There is a small disc of mass \(\displaystyle m\) and of charge \(\displaystyle Q\) on the slope, and a uniform magnetic field of magnitude \(\displaystyle B\) also exerts a force on the moving disc. The magnetic induction is perpendicular to the plane of the slope. The disc is released from rest. Determine the direction and the magnitude of the velocity of the disc, when the velocity becomes constant.

(5 pont)

Deadline expired on January 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelöljük a korong állandósult sebességének nagyságát \(\displaystyle v\)-vel, irányának a lejtő szintvonalaival bezárt szögét \(\displaystyle \beta\)-val (lásd az ábrát, ami a lejtő síkjára merőleges irányú nézet). Az ábrán látható előjelek \(\displaystyle Q>0\) esetén érvényesek. \(\displaystyle Q<0\) (vagy fordított irányú mágneses mező) esetén a korong pályája ellenkező irányban (,,felénk'') térül el.

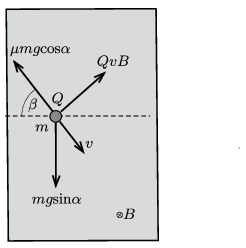
A mozgásegyenletek:

\(\displaystyle mg\sin\alpha\sin\beta=\mu mg\cos\alpha,\)

\(\displaystyle mg\sin\alpha\cos\beta=QvB. \)

A fenti egyenletek négyzetösszegéből

\(\displaystyle v=\frac{mg\cos\alpha}{QB}\sqrt{\tg^2\alpha-\mu^2},\)

az egyenletek arányából pedig

\(\displaystyle \tg\beta=\frac{\mu}{\sqrt{\tg^2\alpha-\mu^2}}\)

következik.

A fenti képletek csak \(\displaystyle \mu<\tg\alpha\) esetben érvényesek. Amennyiben \(\displaystyle \mu>\tg\alpha\), a korong nem jön mozgásba, illetve ha meglökjük, hamarosan megáll, tehát az állandósult sebessége nulla lesz.

Statistics:

39 students sent a solution.
5 points:	Békési Ábel, Bokor Endre, Bonifert Balázs, Bukor Benedek, Csépányi István, Elek Péter, Fiam Regina, Hervay Bence, Keltai Dóra, Kozák 023 Áron, Mácsai Dániel, Markó Gábor, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Morvai Orsolya, Murányi Albert, Olosz Adél, Pácsonyi Péter, Sal Dávid, Somogyi Boglárka Zsófia, Szabó 314 László, Tiefenbeck Flórián, Varga Vázsony, Vaszary Tamás, Viczián Anna.
4 points:	Andorfi István, Hisham Mohammed Almalki, Lipták Gergő, Makovsky Mihály, Szoboszlai Szilveszter, Tafferner Zoltán, Tran Quoc Dat, Vajay Mónika, Vass Bence.
2 points:	1 student.
1 point:	3 students.

Problems in Physics of KöMaL, December 2018