 Problem P. 5094. (January 2019)
Problem P. 5094. (January 2019)
P. 5094. Three point-like objects, each having mass of \(\displaystyle m = 1\) g and charge of \(\displaystyle Q=3.1\cdot 10^{-7}\) C, are attached to one of the ends of three insulating threads of length \(\displaystyle L = 20\) cm (one to each thread). The other ends of the threads are fixed at a common point. Initially the threads were tight and the angle between the vertical and a thread was \(\displaystyle \alpha=30^\circ\), and the small objects were at the vertices of an equilateral triangle. Then the small objects were released at the same instant.
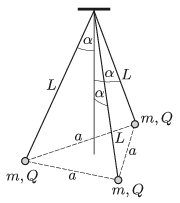
\(\displaystyle a)\) What is the angle between the threads and the vertical when the objects have the greatest speed?
\(\displaystyle b)\) What is the greatest speed of the objects?
(5 pont)
Deadline expired on February 11, 2019.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. \(\displaystyle a)\) Amikor a testek sebessége maximális, akkor a sebességük nagysága nem változik, tehát a rájuk ható eredő erőnek nincsen a sebességükkel párhuzamos komponense.
Az elrendezés szimmetriája miatt a három test mindig szabályos háromszöget alkot, melynek oldalai
\(\displaystyle \ell=\sqrt{3}L\sin\varphi \)
hosszúságúak, ahol \(\displaystyle \varphi\) a fonalaknak a függőlegessel bezárt szöge. (Kezdetben \(\displaystyle \varphi=\alpha\) és \(\displaystyle \ell=a\).)
Tekintsük az egyik testet, amely \(\displaystyle L\) sugarú körpályán mozog. A testre függőlegesen lefelé \(\displaystyle mg\) nehézségi erő, vízszintes irányban (a másik két test által kifejtett) \(\displaystyle \sqrt{3}kQ^2/\ell^2\) nagyságú elektrosztatikus taszítóerő hat. Ezek eredője a legnagyobb sebességnek megfelelő helyzetben fonál irányú, vagyis
\(\displaystyle mg\sin\varphi=\frac{kQ^2}{\sqrt{3}L^2\sin^2\varphi}\cos\varphi\)
teljesül. Ezt az egyenletet
\(\displaystyle \sin^3\varphi=\lambda\,\cos\varphi\)
alakban is felírhatjuk, ahol
\(\displaystyle \lambda=\frac{kQ^2}{\sqrt{3}mgL^2}=1{,}27.\)
A fenti egyenlet \(\displaystyle x=\tg\varphi\) helyettesítéssel harmadfokú egyenletté alakítható:
\(\displaystyle x^2-1{,}27x^2-1{,}27=0,\)
amelynek egyetlen valós gyöke \(\displaystyle x=1{,}704\), azaz
\(\displaystyle \varphi=59{,}6^\circ\approx 60^\circ.\)
\(\displaystyle b)\) A testek legnagyobb sebességét a rendszer összes (mozgási + gravitációs + elektrosztatikus) energiájának állandóságából határozhatjuk meg.
\(\displaystyle -3mgL\cos\alpha+3\frac{kQ^2}{\sqrt{3}L\sin\alpha}=3\cdot\frac{1}{2}mv^2-3mgL\cos\varphi+3\frac{kQ^2}{\sqrt{3}L\sin\varphi},\)
innen az ismert, illetve már kiszámított adatok behelyettesítése után kapjuk, hogy
\(\displaystyle v=1{,}67~\frac{\rm m}{\rm s}.\)
II. megoldás. Az energiamegmaradás tétele szerint (lásd az I. megoldást)
\(\displaystyle \frac{v^2}{6gL}=\left(\cos\varphi- \frac{\sqrt{3}}{2}\right)+\lambda \left(2-\frac{1}{\sin\varphi}\right) \equiv f(\varphi).\)
\(\displaystyle a)\) A legnagyobb sebességű helyzetben az \(\displaystyle f(\varphi)\) deriváltja eltűnik:
\(\displaystyle -\sin\varphi+\lambda\frac{\cos\varphi}{\sin^2\varphi}=0,\)
melynek numerikus megoldása (lásd pl. www.wolframalpha.com): \(\displaystyle \varphi=\varphi_0=59{,}6^\circ.\)
\(\displaystyle b)\) A maximális sebesség: \(\displaystyle v=\sqrt{2gL\cdot f(\varphi_0)}=1{,}67~\frac{\rm m}{\rm s}.\)
Statistics:
38 students sent a solution. 5 points: Bekes Barnabás, Bokor Endre, Csépányi István, Lipták Gergő, Makovsky Mihály, Molnár Mátyás, Sal Dávid, Tiefenbeck Flórián, Vass Bence. 4 points: Hisham Mohammed Almalki, Jánosik Áron, Keltai Dóra, Marozsák Tádé, Máth Benedek, Merkl Gergely, Morvai Orsolya, Németh Csaba Tibor, Olosz Adél, Pácsonyi Péter, Toronyi András, Vaszary Tamás, Viczián Anna, Zámbori Zalán. 3 points: 13 students. 2 points: 2 students.
Problems in Physics of KöMaL, January 2019
