 |
A P. 5123. feladat (2019. április) |
P. 5123. Vízszintes felületen lévő, oldalfalakkal határolt, \(\displaystyle M=1\) kg tömegű, \(\displaystyle L=0{,}3\) m hosszúságú kiskocsi bal oldalán egy \(\displaystyle m=0{,}25\) kg tömegű, kis méretű test található. A kocsi a talajon súrlódásmentesen mozog, kerekeinek mérete és tömege elhanyagolható.
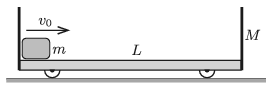
Egy adott pillanatban az \(\displaystyle m\) tömegű testet \(\displaystyle v_0=1\) m/s sebességgel jobbra elindítjuk. A test és a kocsi közötti súrlódási tényező \(\displaystyle \mu=0{,}1\). A test és a kocsi ütközését tekintsük rugalmasnak.
\(\displaystyle a)\) Mekkora sebességgel mozog a kocsi, miután az \(\displaystyle m\) tömegű test a kocsihoz viszonyítva nem mozog?
\(\displaystyle b)\) Milyen távol van ekkor a test a kocsi bal oldali falától?
\(\displaystyle c)\) Mekkora a testek sebessége az első rugalmas ütközés utáni pillanatban?
Közli: Kotek László, Pécs
(5 pont)
A beküldési határidő 2019. május 10-én LEJÁRT.
Megoldás. A test és a kocsi között (ha azok sebessége különböző) \(\displaystyle \mu mg\) nagyságú súrlódási erő hat. \(\displaystyle \mu g\approx 1{,}0~\rm m/s^2\); a továbbiakban ezzel a közelítő értékkel fogunk számolni. \(\displaystyle m\) számszerű értékére nincs szükség, a megoldáshoz csak azt használjuk ki, hogy \(\displaystyle M=4m\).
\(\displaystyle a)\) A kocsi+test rendszerre nem hat vízszintes irányú külső erő, ezért a vízszintes irányú összes lendület állandó marad. Ha a kiskocsi és a hozzá képest nem mozgó test sebessége \(\displaystyle u\), akkor fennáll
\(\displaystyle mv_0=mu+Mu,\qquad \text{azaz}\qquad u=\frac{m}{m+M}v_0=\frac{1}{5}v_0=0{,}2~\frac{\rm m}{\rm s}.\)
\(\displaystyle b)\) Írjuk fel a munkatételt a kezdeti és a végállapot között! A súrlódási erő munkáját a kiskocsi és a test \(\displaystyle x\) nagyságú relatív elmozdulása határozza meg (1. ábra):
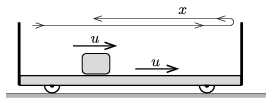
1. ábra
\(\displaystyle \frac{1}{2}(M+m)u^2-\frac{1}{2}mv_0^2=-\mu mgx,\)
ahonnan
\(\displaystyle x=\frac{2}{5}\,\frac{v_0^2}{\mu g}=0{,}4~{\rm m}=2L-0{,}2~{\rm m.}\)
Az \(\displaystyle m\) tömegű test tehát a kocsi bal oldali szélétől 20 cm távolságban lesz, amikor a relatív sebességük nullára csökken.
\(\displaystyle c)\) Legyen a kis test sebessége \(\displaystyle v_1\), a kocsi sebessége pedig \(\displaystyle v_2\) akkor, amikor a kis test eléri a kocsi jobb oldali szélét! (A sebességek irányát \(\displaystyle v_0\)-lal megegyező irányban tekintjük pozitívnak (2. ábra).)
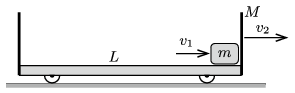
2. ábra
A lendületmegmaradás törvénye szerint
\(\displaystyle mv_0=mv_1+(4m)v_2,\)
a munkatétel pedig így alkalmazható:
\(\displaystyle \frac{1}{2}mv_1^2+\frac{1}{2}(4m)v_2^2-\frac{1}{2}mv_0^2=-\mu mgL.\)
(Ismét kihasználtuk, hogy a súrlódási erők munkájánál csak a két test relatív elmozdulását kell figyelembe vennünk.) A fenti egyenletek (ha az SI-mértékegységeket nem írjuk ki) igy alakulnak:
\(\displaystyle 1=v_1+4v_2,\)
\(\displaystyle 1=v_1^2+4v_2^2+0{,}6.\)
Ennek az egyenletrendszernek az egyik megoldása:
\(\displaystyle v_1=0{,}6~\frac{\rm m}{\rm s} \qquad \text{és}\qquad v_2=0{,}1~\frac{\rm m}{\rm s},\)
ami \(\displaystyle v_1>v_2\) miatt az ütközés előtti viszonyokat írja le. A másik megoldás:
\(\displaystyle v_1=-0{,}2~\frac{\rm m}{\rm s} \qquad \text{és}\qquad v_2=0{,}3~\frac{\rm m}{\rm s},\)
ami \(\displaystyle v_1<v_2\) miatt az ütközés utáni sebességeket adja meg.
Statisztika:
37 dolgozat érkezett. 5 pontot kapott: Békési Ábel, Bokor Endre, Elek Péter, Fonyi Máté Sándor, Jánosik Áron, Keltai Dóra, Kertész Balázs, Mácsai Dániel, Makovsky Mihály, Markó Gábor, Marozsák Tádé, Merkl Gergely, Molnár Mátyás, Olosz Adél, Pácsonyi Péter, Sal Dávid, Tiefenbeck Flórián, Toronyi András, Varga Vázsony, Vass Bence, Vaszary Tamás, Viczián Anna. 4 pontot kapott: Schneider Anna. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 6 versenyző.
A KöMaL 2019. áprilisi fizika feladatai
