 |
A P. 5124. feladat (2019. április) |
P. 5124. \(\displaystyle a)\) Vízszintes asztallapra két egyforma, tömör hengert helyezünk közvetlenül egymás mellé, majd óvatosan egy ugyanilyen, harmadik hengert rakunk rájuk. Legalább mekkora legyen a hengerek közötti, illetve a hengerek és az asztal közötti súrlódási együttható, hogy ez az elrendezés egyensúlyban maradhasson?
\(\displaystyle b)\) Vízszintes asztallapra három egyforma, tömör gömböt helyezünk közvetlenül egymás mellé, majd óvatosan egy ugyanilyen, negyedik gömböt rakunk rájuk. Legalább mekkora legyen a gömbök közötti, illetve a gömbök és az asztal közötti súrlódási együttható, hogy ez az elrendezés egyensúlyban maradhasson?

Közli: Vass Miklós, Budapest
(5 pont)
A beküldési határidő 2019. május 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Ha elegendően nagy a súrlódás, a két alsó henger egymásnak feszülhet, és ez megnöveli az asztalnál ható súrlódási erőt. Az egyensúlyhoz szükséges legkisebb súrlódási együtthatót úgy kapjuk meg, ha ilyen ,,egymásnak-feszülés'' nem lép fel, vagyis az alsó hengerek között egy hajszálnyi távolság van, és a hengerek között nem hat erő.
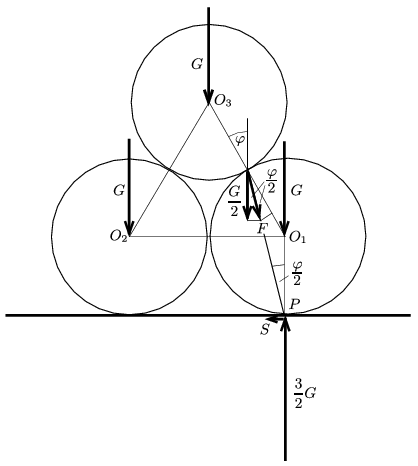
1. ábra
Tekintsük a három henger nézetét a tengelyük irányából (1. ábra). A körlapok \(\displaystyle O_1\), \(\displaystyle O_2\) és \(\displaystyle O_3\) középpontja szabályos háromszöget alkot, így \(\displaystyle \varphi=30^\circ\). A felső henger az egyik (mondjuk a jobb oldali) alsóra olyan \(\displaystyle \boldsymbol F\) erőt (nyomó- és súrlódási erő eredője) fejt ki, amely áthalad az asztal \(\displaystyle P\) pontján (hiszen a jobb oldali hengerre ható másik két erő, a súlyerő és az asztal által kifejtett erő is ezen a ponton halad át). A felső henger által kifejtett erő tehát \(\displaystyle \varphi/2=15^\circ\)-os szöget zár be a felületek normálisával, így a hengerek közötti súrlódási együtthatóra a
\(\displaystyle \mu_\text{fent}\ge \tg\frac\varphi2=\tg 15^\circ\approx0{,}27\)
feltételt kapjuk.
A \(\displaystyle G\) súlyú felső henger függőleges irányban \(\displaystyle G/2\) erőt fejt ki mindkét alsó hengerre, tehát az \(\displaystyle \boldsymbol F\) erő függőleges komponense \(\displaystyle G/2\). Ugyanekkora az \(\displaystyle \boldsymbol F\) erő normális komponense is, hiszen a függőlegessel és az érintőfelület normálisával bezárt szöge ugyanakkora, nevezetesen \(\displaystyle \varphi/2\). Eszerint a súrlódási erő a felső és az alsó henger között (ami \(\displaystyle \boldsymbol F\) érintő irányú komponense)
\(\displaystyle S=\frac{G}{2}\tg\frac\varphi2,\)
és ugyanekkora nagyságú \(\displaystyle \boldsymbol F\) vízszintes irányú összetevője is.
Az asztal és az alsó henger között ható (vízszintes irányú) súrlódási erő ugyancsak \(\displaystyle S\) nagyságú, amint az akár az alsó hengerre ható eredő forgatónyomaték, akár az alsó hengerre ható eredő vízszintes erő eltűnéséből következik. Az asztal függőleges irányban \(\displaystyle N=\frac{3}{2}G\) erőt fejt ki egy-egy alsó hengerre, így azok el nem csúszásának feltétele:
\(\displaystyle \mu_\text{lent}\ge\frac{S}{N}=\frac{1}{3}\tg\frac\varphi2\approx0{,}09.\)
\(\displaystyle b)\) A hengerekéhez hasonló módon számíthatjuk ki 4 gömb egyensúlyának feltételét is. A gömbök középpontjai szabályos tetraédert alkotnak, és tekinthetjük úgy, hogy az asztalon fekvő három gömb éppen nem ér egymáshoz, tehát erőt sem fejtenek ki egymásra.
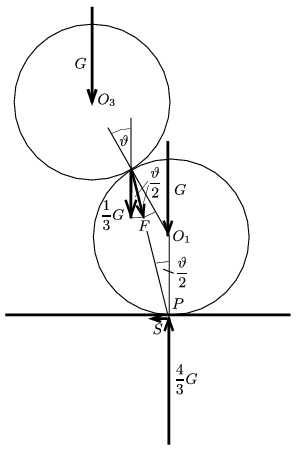
2. ábra
Tekintsük a felső gömb és az egyik kiválasztott alsó gömb olyan irányú nézetét, amelyben ezen két gömb vetülete éppen érinti egymást (2. ábra). A szabályos tetraéder geometriájából következik, hogy
\(\displaystyle \sin\vartheta=\frac{1}{\sqrt{3}}, \qquad \text{tehát} \qquad \vartheta\approx 35{,}26^\circ.\)
A felső gömb által az alsóra kifejtett erő \(\displaystyle \vartheta/2\) szöget zár be a felületi normálissal, a csúszásmentesség feltétele tehát
\(\displaystyle \mu_\text{fent}\ge \tg\frac\vartheta2=\sqrt{3}-\sqrt{2} \approx0{,}32.\)
A \(\displaystyle G\) súlyú felső gömb függőleges irányban \(\displaystyle G/3\) erőt fejt ki mindhárom alsó gömbre, így a súrlódási erő a felső és az alsó gömbök között
\(\displaystyle S=\frac{G}{3}\tg\frac\vartheta2.\)
Ugyanekkora súrlódási erő hat az asztal és az alsó gömbök bármelyike között (hiszen az alsó gömbökre ható eredő forgatónyomaték nulla). Az asztal függőleges irányban \(\displaystyle N=\frac{4}{3}G\) erőt fejt ki az egyes gömbökre, így az el nem csúszás feltétele:
\(\displaystyle \mu_\text{lent}\ge\frac{S}{N}=\frac{1}{4}\tg\frac\vartheta2\approx0{,}08.\)
Statisztika:
16 dolgozat érkezett. 5 pontot kapott: Fiam Regina, Makovsky Mihály, Markó Gábor, Máth Benedek, Olosz Adél, Sal Dávid, Tiefenbeck Flórián. 4 pontot kapott: Hervay Bence, Lipták Gergő, Marozsák Tádé, Vass Bence. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2019. áprilisi fizika feladatai
