A P. 5125. feladat (2019. április)

P. 5125. Egy \(\displaystyle \alpha=30^\circ\) hajlásszögű, súrlódó lejtő érintőlegesen csatlakozó, \(\displaystyle R=32\) cm sugarú hengerfelületben folytatódik az ábra szerint. A henger keresztmetszete a \(\displaystyle T\) talpponttól mérve háromnegyed körívet alkot. A hengerfelület ideálisan sima. A lejtőre helyezett \(\displaystyle r\) sugarú, \(\displaystyle m\) tömegű, homogén, tömör korongot lökésmentesen elengedjük. (A tapadási súrlódás elegendően nagy, a korong nem csúszik meg a lejtőn. A gördülő ellenállás elhanyagolható.)

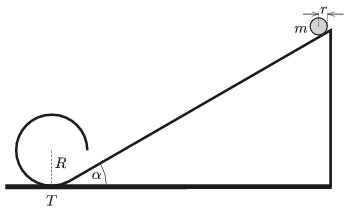
\(\displaystyle a)\) Mekkora a korong sugara, ha az éppen átfér a hengerfelület alatt?

\(\displaystyle b)\) A talajtól mérve legalább milyen magasról kell indítani a korongot, hogy az függőleges irányú sebességgel érkezzen vissza a lejtőre?

\(\displaystyle c)\) Ebben az esetben mekkora sebességgel éri el a lejtőt?

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2019. május 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) Az 1. ábráról leolvasható, hogy ha a korong éppen átfér a hengerfelület alatt, akkor

\(\displaystyle R=R\sin\alpha+2r,\)

vagyis

\(\displaystyle r=R \frac{1-\sin\alpha}{2} =\frac{R}{4}=8~\rm cm.\)

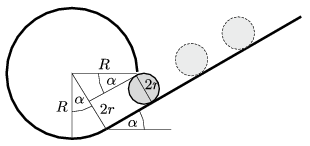
1. ábra

\(\displaystyle b)\) Legyen \(\displaystyle H\) a korong középpontjának magassága a vízszintes talajtól mérve az elengedés pillanatában. Itt a korong helyzeti energiája \(\displaystyle mgH\). A \(\displaystyle H\) magasságból induló korong a lejtőn gördül, a lejtő egyenes részének alján (ha ott a tömegközéppontjának sebessége \(\displaystyle v_0\))

\(\displaystyle E_1= \frac{1}{2}mv_0^2\)

transzlációs mozgási és

\(\displaystyle E_2= \frac{1}{2}\Theta \omega^2= \frac{1}{4}mv_0^2\)

forgási energiával rendelkezik. Az energiamegmaradás tétele szerint

\(\displaystyle mgH-mgR+mg(R-r)\cos\alpha =E_1+E_2.\)

A mozgás további részében a hengerfelület simasága miatt a forgási energia nem változik, ezért elegendő csak a transzlációs mozgás energiájával foglalkoznunk. A tömegközéppont \(\displaystyle R-r=0{,}24~\rm m\) sugarú körpályán mozog, és akkor nem válik el a körívtől annak legmagasabb pontjánál, ha az ottani \(\displaystyle v\) sebességére fennáll:

\(\displaystyle m\frac{v^2}{R-r}\ge mg.\)

A munkatétel szerint

\(\displaystyle m\frac{v^2}{2}=m\frac{v_0^2}{2}-mg(R-r)(1+\cos\alpha).\)

A fenti egyenletekből kapjuk, hogy

\(\displaystyle H\ge \frac{13}{4}R - \frac{9}{4}r + \frac{1}{2}(R-r)\,\cos\alpha=0{,}964~\rm m. \)

\(\displaystyle c)\) A hengerfelülettel érintkező korong tömegközéppontja a körpálya legmagasabb pontjánál

\(\displaystyle v=\sqrt{(R-r)g}\approx 1{,}53~\rm m/s\)

sebességgel mozog. Innen a körpálya végéig a tömegközéppont \(\displaystyle h_1\) távolságnyival kerül mélyebbre, majd függőleges hajítással mozogva a lejtőig további \(\displaystyle h_2\)-t süllyed. A munkatétel szerint a lejtőnek ütköző korong tömegközéppontjának sebessége

\(\displaystyle v_\text{ütk}=\sqrt{v^2+2g(h_1+h_2)}.\)

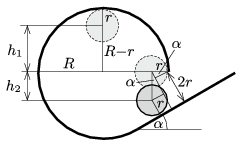
2. ábra

A 2. ábráról leolvasható, hogy

\(\displaystyle h_1=R-r=0{,}24~\rm m,\)

továbbá

\(\displaystyle 2r+r\sin\alpha=h_2\cos\alpha+r,\)

vagyis

\(\displaystyle h_2=\frac {1+\sin\alpha}{\cos\alpha}r\approx 0{,}14~\rm m,\)

és így a keresett sebesség: \(\displaystyle v_\text{ütk}\approx 3{,}13~\frac{\rm m}{\rm s}.\)

Statisztika:

44 dolgozat érkezett.
4 pontot kapott:	Makovsky Mihály.
3 pontot kapott:	11 versenyző.
2 pontot kapott:	17 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2019. áprilisi fizika feladatai