 |
A P. 5131. feladat (2019. április) |
P. 5131. Három azonos, állandó hőkapacitású test közül kettőnek a hőmérséklete 300 K, a harmadiké 100 K. Fel lehet-e melegíteni valamelyik testet 400 K hőmérsékletre külső hő és munka befektetése nélkül, csupán termodinamikai gépeket (hőerőgép, hűtőgép) működtetve a testek között?
Közli: Radnai Gyula, Budapest
(6 pont)
A beküldési határidő 2019. május 10-én LEJÁRT.
I. megoldás. Jelöljük a hidegebb test kezdeti 100 K-es hőmérsékletét \(\displaystyle T_0\)-lal, a másik két test hőmérséklete ekkor \(\displaystyle 3T_0\). Működtessünk az egyik melegebb test és a hidegebb test segítségével egy ideális Carnot-féle hőerőgépet. Legyen a két test (lassan változó) hőmérséklete \(\displaystyle T_1\) és \(\displaystyle T_2\), a hőmérséklet kicsiny megváltozása pedig \(\displaystyle \Delta T_1<0\) és \(\displaystyle \Delta T_2>0\). A leadott és a felvett hő a hőkapacitások egyenlősége miatt a hőmérséklet-változással arányos. Ideális esetben (a legnagyobb elérhető hatásfoknál)
\(\displaystyle \frac{\Delta T_1}{T_1}+\frac{\Delta T_2}{T_2}=\frac{\Delta (T_1T_2)}{T_1T_2}=0,\)
vagyis \(\displaystyle \Delta (T_1T_2)=0\), azaz
\(\displaystyle T_1T_2=\text{állandó}=3T_0^2.\)
A hőerőgép működése addig tart, amíg el nem érjük a \(\displaystyle T_1=T_2=T^*=\sqrt{3}\,T_0\) hőmérsékleti egyensúlyi állapotot (1. ábra). A gép a működése során
\(\displaystyle W=C(T_0+3T_0)-2C\,\sqrt{3}\,T_0=(4-2\sqrt{3})CT_0\)
nagyságú hasznosítható munkát végez, amit (pl. elektromos formában, akkumulátorok feltöltésével) tárolhatunk. (\(\displaystyle C\) a testek egymással megegyező hőkapacitását jelöli.)
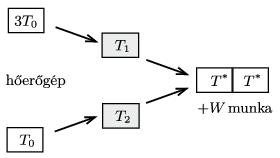
1. ábra
Használjuk fel a \(\displaystyle W\) munkát arra, hogy a másik melegebb (kezdetben \(\displaystyle 3T_0\) hőmérsékletű) testet a két hidegebb (kezdetben \(\displaystyle \sqrt{3}T_0\) hőmérsékletű) test lehűlésével kísérve valamennyire felmelegítjük. Ezt legnagyobb hatásfokkal egy fordított Carnot-gépként működő hőszivattyú segítségével tehetjük meg (2. ábra). A testek hőmérsékletét \(\displaystyle T_3\)-mal és \(\displaystyle T_4\)-gyel jelölve felírhatjuk, hogy
\(\displaystyle \frac{Q_3}{T_3}+\frac{Q_4}{T_4}=0,\qquad \text{azaz}\qquad \frac{\Delta T_3}{T_3}+2\frac{\Delta T_4}{T_4}=\frac{\Delta\left(T_3T_4^2\right)}{T_3T_4^2}=0.\)
(A 2-es szorzótényező azt fejezi ki, hogy a hidegebb test tömege 2-szerese a melegebbének.) Ezek szerint a hőszivattyú kezdeti állapotát is figyelembe véve
\(\displaystyle T_3T_4^2=\text{állandó}=9T_0^3.\)
A hőszivattyú működése addig tart, amíg fel nem használjuk a hőerőgép által termelt \(\displaystyle W\) munkát.
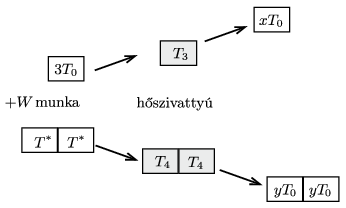
2. ábra
Jelöljük a legmelegebb test végső hőmérsékletét \(\displaystyle xT_0\)-lal, a két hidegebb test végső hőmérsékletét pedig \(\displaystyle yT_0\)-lal! A fenti összefüggések szerint
| \(\displaystyle (1)\) | \(\displaystyle xy^2=9.\) |
Hőszivattyú esetén a munka
\(\displaystyle W=C(xT_0-3T_0)-2C(\sqrt(3)T_0-yT_0)=CT_0(x-3-2\sqrt{3}+2y),\)
ami akkor egyezik meg a hőerőgépből nyert munkával, ha fennáll:
| \(\displaystyle (2)\) | \(\displaystyle x+2y=7.\) |
A feladat eredeti kérdése: elérhető-e a 400 K-es csúcshőmérséklet, vagyis megoldása-e az (1) és (2) egyenletrendszernek \(\displaystyle x=4\)? Behelyettesítéssel igazolható, hogy igen, és a hozzá tartozó \(\displaystyle y\) értéke 1,5, vagyis a másik két test hőmérséklete ebben az állapotban 150 K lesz.
Megjegyzés. Felmerül a kérdés: Vajon elérhető-e a leírt módon 400 K-nél magasabb hőmérséklet? A válasz: Nem! Az egyik test legmelegebb állapotában a másik két test hőmérséklete ugyanakkora kell legyen; ellenkező esetben azokkal egy hőerőgépet működtetve további hasznos munkát lehetne ,,nyerni''. Két egyforma és egy tőlük különböző hőmérsékletű testekre fennáll az (1) és (2) egyenletrendszer. Ennek az (\(\displaystyle y\) kiküszöbölése után \(\displaystyle x\)-re nézve
\(\displaystyle x^3-14x^2+49 x-36=0\)
harmadfokú) egyenletnek nyilvánvaló megoldása \(\displaystyle x=1\), ami a kezdeti állapotnak felel meg. Az \(\displaystyle x-1\) gyöktényezővel osztva egy másodfokú egyenletet kapunk, amelynek egyik gyöke a feladat szempontjából érdekes \(\displaystyle x=4\), a másik pedig \(\displaystyle x=9\). Ez utóbbihoz \(\displaystyle y=-1\) tartozik, ami nem ír le fizikailag értelmes megoldást.
Az adott kezdeti feltételek mellett tehát valóban 400 K a legmagasabb elérhető hőmérséklet, és az is csak ideális körülmények között (ideális Carnot-gépek és 100%-os energiatárolási hatásfok) esetén lenne létrehozható.
II. megoldás. A testek azonos, állandó hőkapacitását \(\displaystyle C\)-vel jelölve egy-egy test belső energiája
\(\displaystyle U=CT.\)
Mivel a három testből álló rendszer energetikailag zárt, ezért az összenergia állandó:
\(\displaystyle U_1+U_2+U_3=C\left(T_1+T_2+T_3\right)=\text{állandó},\)
vagyis az abszolút hőmérsékletek összege sem változhat.
Másrészt a hőerőgép és a hűtőgép (reverzibilis) működése közben nem változhat a hőtartályok entrópiájának összege:
\(\displaystyle S_1+S_2+S_3 =\text{állandó.}\)
Egy-egy test entrópiája így számítható ki:
\(\displaystyle S=\int \frac{{\rm d}Q}{T}=\int \frac{{C\rm d}T}{T}=C\int \frac{{\rm d}T}{T}=C\ln T+\text{állandó}.\)
Nem változhat tehát a következő összeg sem:
\(\displaystyle C\ln T_1+C\ln T_2+C\ln T_3= C\ln \left(T_1T_2T_3\right).\)
Ez csak úgy lehet, ha az abszolút hőmérsékletek szorzata is állandó marad.
Feladatunkban \(\displaystyle T_1=T_2=300~\rm K\), \(\displaystyle T_3=100~\rm K\). Olyan új \(\displaystyle T_1'\), \(\displaystyle T_2'\) és \(\displaystyle T_3'\) hőmérsékletek érhetők el tehát, amelyekre
\(\displaystyle T_1'+T_2'+T_3'=700~{\rm K}\qquad \text{és}\qquad T_1' T_2' T_3'= 9\cdot10^6~{\rm K}^3.\)
Áttekinthetőbb lesz a számolás, ha 100 K-es egységekben, vagyis
\(\displaystyle T_1=x\cdot 100~{\rm K},\quad T_2=y\cdot 100~{\rm K},\quad T_3=z\cdot 100~{\rm K}\)
alakban keressük a megoldást. Ezzel az
\(\displaystyle x+y+z=7 \quad \text{és}\quad xyz=9\)
egyenletrendszerhez jutunk. Arra vagyunk kiváncsiak, lehetséges-e \(\displaystyle z=4\) mellett két egyenlő, pozitív gyöke ennek az egyenletrendszernek. Jelöljük ezt a gyököt \(\displaystyle x\)-szel, ekkor
\(\displaystyle x+x+4=7 \quad \text{és}\quad x\cdot x\cdot 4=9\)
lehetséges (pozitív) megoldását keressük, amely pedig \(\displaystyle x=1{,}5.\)
Az új hőmérsékletek tehát 150 K, 150 K és 400 K.
Megjegyzés. A testek azonos, állandó (a hőmérsékletüktől nem függő) hőkapacitását \(\displaystyle C\)-vel jelölve egy-egy test belső energiája
\(\displaystyle U=CT.\)
Mivel a három testből álló rendszer energetikailag zárt, ezért az összenergia állandó:
\(\displaystyle U_1+U_2+U_3=C\left(T_1+T_2+T_3\right)=\text{állandó},\)
vagyis az abszolút hőmérsékletek összege nsem változhat.
Másrészt a hőerőgép és a hűtőgép működése közben nem csökkenhet a rendszer entrópiája (a három test entrópiájának összege), reverzibilis folyamatok során pedig az entrópia változatlan marad:
\(\displaystyle S_1+S_2+S_3 =\text{állandó, vagy növekszik}.\)
Egy-egy test entrópiája így számítható ki:
\(\displaystyle S=\int \frac{{\rm d}Q}{T}=\int \frac{{C\rm d}T}{T}=C\int \frac{{\rm d}T}{T}=C\ln T+\text{állandó}.\)
Nem csökkenhet (reverzibilis folyamatban nem változhat) tehát a
\(\displaystyle C\ln T_1+C\ln T_2+C\ln T_3= C\ln \left(T_1T_2T_3\right)\)
összeg, ami csak úgy lehetséges, ha az abszolút hőmérsékletek szorzata nem csökken.
Feladatunkban \(\displaystyle T_1=T_2=300~\rm K\), \(\displaystyle T_3=100~\rm K\). Olyan új \(\displaystyle T_1'\), \(\displaystyle T_2'\) és \(\displaystyle T_3'\) hőmérsékletek érhetők el tehát, amelyekre
\(\displaystyle T_1'+T_2'+T_3'=700~{\rm K}\qquad \text{és}\qquad T_1' T_2' T_3'\ge 9\cdot10^6~{\rm K}^3.\)
Áttekinthetőbb lesz a számolás, ha 100 K-es egységekben, vagyis
\(\displaystyle T_1=x\cdot 100~{\rm K},\quad T_2=x\cdot 100~{\rm K},\quad T_1=z\cdot 100~{\rm K}\)
alakban keressük a megoldást. Ezzel az
\(\displaystyle x+y+z=7, \qquad xyz\ge9\)
feltételekhez, vagy – mondjuk – \(\displaystyle z\) kiküszöbölése után a
| \(\displaystyle (3)\) | \(\displaystyle (7-x-y)xy\ge 9\) |
egyenlőtlenséghez jutunk. Fennáll még, hogy \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) mindegyike pozitív szám, vagyis
| \(\displaystyle (4).\) | \(\displaystyle x>0, \quad y>0\quad \text{és} \quad x+y<7.\) |
Ábrázoljuk (például a www.wolframalpha.com program segítségével) a (3) és (4) egyenlőtlenségnek megfelelő értékeket az \(\displaystyle x-y\) koordináta-rendszerben! Így a 3. ábrán sötétebben jelölt tartományt kapjuk, amelynek határvonala a reverzibilis állapotváltozásnak felel meg. A kezdeti állapot a változók háromféle lehetséges szereposztásának megfelelően a \(\displaystyle K_1\), \(\displaystyle K_2\) és \(\displaystyle K_3\) pontok valamelyike, a végállapot pedig (amelyben valamelyik test hőmérséklete maximális) a \(\displaystyle V_1\), \(\displaystyle V_2\) és \(\displaystyle V_3\) pontok egyike. A 3. ábráról leolvasható, hogy bármelyik test legmagasabb hőmérséklete 400 K lehet, és ilyenkor a másik két test 150 K-es. (Az is kiderül az ábráról, hogy egy-egy test legalacsonyabb hőmérséklete 100 K lehet, és ebben az állapotban a másik két test 300 K-es, ahogy ez a kezdeti állapotban volt.)
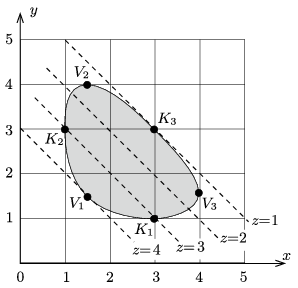
3. ábra
A rendszer – megfelelő hűtőgép és hőerőgép folyamatos működtetésével – úgy juthat el valamelyik \(\displaystyle K_i\) kezdőállapotból az egyik \(\displaystyle V_j\) végállapotba, hogy közben az összentrópia állandó marad, vagyis a rendszer az \(\displaystyle x-y\) síkon a sötét terület határvonala mentén ,,mozog''. Ha valahol bejutna a rendszer a sötét tartomány belsejébe (vagyis az entrópia növekedésével járó irreverzibilis folyamat is végbemenne), akkor már biztosan nem kerülhetne vissza vissza az alacsonyabb entrópiájú határgörbére, vagyis nem érhetné el a kívánt 400 K-es állapotot.
Statisztika:
5 dolgozat érkezett. 6 pontot kapott: Elek Péter. 5 pontot kapott: Markó Gábor. 3 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2019. áprilisi fizika feladatai
