A P. 5156. feladat (2019. október)

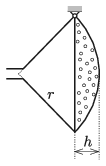
P. 5156. Vékony lemezből készült öntözőkanna gömbcikk alakú rózsáját peremkörének egyik pontjánál az ábrán látható módon csuklósan rögzítettük. Mekkora a $\displaystyle h/r$ arány, ha egyensúlyi állapotban a test tengelye vízszintes? (A vékony lemez homogén, állandó vastagságú. A rózsa vízbevezető csövecskéjének méretét és a kifolyónyílások összes területét tekintsük elhanyagolhatóan kicsinek.)

Közli: Németh László, Fonyód

(5 pont)

A beküldési határidő 2019. november 11-én LEJÁRT.

Megoldás. Jelöljük a vékony lemez egységnyi felületű darabjának tömegét (felületi tömegsűrűségét) $\displaystyle \eta$-val, a peremkörének sugarát pedig $\displaystyle R$-rel. Ez utóbbi kifejezhető $\displaystyle r$-rel és $\displaystyle h$-val:

$\displaystyle R^2+(r-h)^2=r^2,\qquad \text{vagyis}\qquad R=\sqrt{h(2r-h)}.$

A locsolókanna-rózsa gömbszelet alakú részének tömege

$\displaystyle m_1=\eta 2r\pi h,$

és ennek a résznek a tömegközéppontja

$\displaystyle x_1=\frac{h}{2}$

távol esik a csuklón átmenő és a szimmetriatengelyre merőleges síktól.

A locsolókanna-rózsa kúppalást alakú részének tömege

$\displaystyle m_2=\eta r\pi \sqrt{h(2r-h)},$

és a tömegközéppont távolsága az előbb említett síktól

$\displaystyle x_2=\frac{r-h}{3}.$

Megjegyzés. A tömegközéppont helyét pl. úgy is megkaphatjuk, hogy összehasonlítjuk a képzeletben egyenletes vastagságú részekre szeletelt kúppalást egyes darabjaira ható nehézségi erőt egy – ugyancsak egyenközűen felszeletelt – derékstögű háromszög alakú lemez részeire ható erővel. Mindkét esetben a nehézségi erő nagysága a szeletek sorszámával arányosan, lineárisan változik, tehát mindkét alakzat tömegközéppontja ugyanott, a magasság egyharmadánál lesz.

A kanna rózsája akkor maradhat egyensúlyban vízszintes szimmetriatengellyel, ha a csuklóra vonatkoztatva a két rész súlyának forgatónyomatéka megegyezik:

$\displaystyle m_1gx_1=m_2gx_2,$

azaz

$\displaystyle 2\pi r h \cdot \frac{h}{2}\cdot \eta g= r\pi \sqrt{h(2r-h)}\cdot \frac{r-h}{3}\cdot \eta g.$

Ebből a $\displaystyle \lambda=h/r$ dimenziótlan arányszámra (algebrai átalakítások után) a

$\displaystyle 10\lambda^3-4\lambda^2+5\lambda-2\equiv (5\lambda-2)(2\lambda^2+1)=0$

harmadfokú egyenletet kapjuk. Látható, hogy ennek egyetlen valós gyöke:

$\displaystyle \lambda=\frac{2}{5}=0{,}4.$

Statisztika:

25 dolgozat érkezett.
5 pontot kapott:	Bohács Tamás, Bokor Endre, Bonifert Balázs, Fülöp Sámuel Sihombing, Pálfi Fanni, Pankotai Dóra Anna, Somlán Gellért, Vass Bence.
4 pontot kapott:	Varga Vázsony.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	7 versenyző.

A KöMaL 2019. októberi fizika feladatai