 Problem P. 5188. (January 2020)
Problem P. 5188. (January 2020)
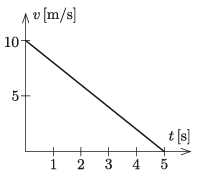
P. 5188. A cuboid-shaped prism is sliding along a horizontal surface in a straight line and is decelerating due to friction. The figure shows the velocity-time graph of its motion.
A spring-loaded toy cannon is attached to the top of the prism, which fires projectiles of mass \(\displaystyle m\) at a speed of \(\displaystyle v_0\), during the slowing motion of the prism. The total mass of the prism and the toy cannon is \(\displaystyle M\).
\(\displaystyle a)\) To which direction should the cannon be aimed in order that the projection not affect the decelerating motion of the prism, or in other words the graph of the motion of the cannon continue in the same way after firing the projectile?
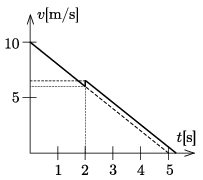
\(\displaystyle b)\) If the angle between the gun barrel and the horizontal is adjusted to half of the angle determined in the previous problem, then how does this affect the graph of the deceleration? Sketch the modified velocity-time graph of the motion, if the projectile was shot at \(\displaystyle t=2\) s.
Data: \(\displaystyle m=0.1\) kg, \(\displaystyle M=1\) kg, \(\displaystyle v_0=5\) m/s.
(5 pont)
Deadline expired on February 10, 2020.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A grafikonról leolvasható, hogy a hasáb gyorsulása: \(\displaystyle a=\mu g=-2~\frac{\rm m}{\rm s^2}\approx 0{,}2\,g\), tehát a csúszási súrlódási együttható közelítőleg 0,2. (A pontosabb érték: 0,204.) A hasábra a vízszintes felület olyan erőt fejt ki, amely a függőlegessel (a hasáb haladási irányához képest ,,hátrafelé'') \(\displaystyle \varphi=\arctg \mu=11{,}31^\circ\text{-os}\) szöget zár be.
A pillanatszerűnek tekintett (valójában csak nagyon rövid ideig tartó) kilövés során a lövedék hirtelen felgyorsul, tehát igen rövid \(\displaystyle \Delta t\) ideig nagyon nagy \(\displaystyle \boldsymbol F\) erő hat rá. A hasábra ugyancsak egy nagy erőlökés hat (amit a vízszintes felület fejt ki), ez akadályozza meg, hogy a hasáb függőleges irányban elmozduljon. A hasábra ható erőlökés iránya a függőlegessel ugyancsak \(\displaystyle \varphi\) szöget zár be, hiszen azt az \(\displaystyle \boldsymbol N\) nyomóerő és az \(\displaystyle \boldsymbol S\) súrlódási erő eredője hozza létre. A lendületmegmaradás törvénye szerint
| \(\displaystyle (1)\) | \(\displaystyle \boldsymbol F \Delta t=m{ \boldsymbol v}_\text{lövedék}+M\Delta{ \boldsymbol v}_\text{hasáb}.\) |
\(\displaystyle a)\) Amennyiben a kilövés nincs hatással a hasáb mozgására (vagyis nem változik meg hirtelen a hasáb sebessége), akkor \(\displaystyle \Delta{ \boldsymbol v}_\text{hasáb}=0\), és így \(\displaystyle \boldsymbol F\) és \(\displaystyle \boldsymbol v_\text{lövedék}\) azonos irányú vektorok. Az előbbi a függőlegessel \(\displaystyle \varphi\) szöget zár be, a lövedék sebességét pedig az ágyúcső függőlegessel bezárt \(\displaystyle \gamma\) szöge határozza meg. Az (1) egyenlet csak akkor teljesülhet, ha \(\displaystyle \gamma=\varphi\), vagyis az ágyúcső a vízszintessel \(\displaystyle 90^\circ-\varphi=78{,}47^\circ\)-os szöget zár be.
Megjegyzés. A kilőtt lövedék sebességének benne kell lennie a hasáb sebessége és a függőleges által meghatározott síkban. Ha az ágyúcső ,,ferdén'' állna, akkor a lövedék ,,oldalirányú'' lendülete megváltoztatná a hasáb mozgásának irányát.
\(\displaystyle b)\) Változtassuk meg most az ágyúcsőnek a vízszintessel bezárt szögét az előző esetbeli szög felére, \(\displaystyle 39{,}23^\circ\)-ra, vagyis legyen az ágyúcső és a függőleges szöge \(\displaystyle \gamma'=50{,}77^\circ\).
A kilövés pillanatában (\(\displaystyle t=2~\rm s\)-nál az \(\displaystyle M+m\) tömegű rendszer \(\displaystyle v_1=6\) m/s sebességgel mozog, tehát a lendülete \(\displaystyle (M+m)v_1\). A kilövés hatására a hasáb sebessége hirtelen megváltozik, nagysága \(\displaystyle v_2\) lesz. Az \(\displaystyle m\) tömegű lövedék a hasábhoz képest \(\displaystyle v_0\cos\gamma'\) függőleges irányú és \(\displaystyle -v_0\sin\gamma'\) vízszintes irányú sebességre tesz szert. A lövedék vízszintes sebességkomponense a talajhoz képest \(\displaystyle v_2-v_0\sin\gamma'\) nagyságú. A függőleges irányú lendületváltozást az
\(\displaystyle N\Delta t=mv_y\)
erőlökés hozta létre. A vízszintes irányú erőlökés:
\(\displaystyle S\Delta t=-\mu N \Delta t= -\mu m v_y.\)
A vízszintes irányú lendületváltozást leíró egyenlet:
\(\displaystyle (Mv_2+m(v_2-v_0\sin\gamma')-(M+m)v_1= -\mu m v_0\cos\gamma',\)
ahonnan a hasáb sebességváltozása:
\(\displaystyle v_2-v_1=\frac{m}{M+m}v_0\cos\gamma'(\tg\gamma'-\mu).\)
(Látható, hogy ha \(\displaystyle \tg\gamma'=\mu\) teljesülne, akkor nem változna meg a hasáb sebessége a kilövés következtében, ahogy ezt már korábban beláttuk.) A leeresztett csövű ágyúnál viszont \(\displaystyle v_2-v_1=0{,}294~{\rm m/s}\approx 0{,}3~{\rm m/s}\), tehát a hasáb sebessége a kilövés hatására 6,3 m/s-ra nő. A hasáb a további mozgása során ugyanolyan ütemben lassul, mint korábban (hiszen a súrlódás miatti fékeződés üteme nem függ a mozgó test tömegétől).
Statistics:
33 students sent a solution. 4 points: Nguyễn Đức Anh Quân. 3 points: 11 students. 2 points: 6 students. 1 point: 5 students. 0 point: 10 students.
Problems in Physics of KöMaL, January 2020
