A P. 5198. feladat (2020. február)

P. 5198. Hasáb alakú, $\displaystyle M$ tömegű test nyugszik egy vízszintes, sima lapon. Egy $\displaystyle D$ rugóállandójú, a hasáb hossztengelyével párhuzamos, könnyű rugó egyik végét a hasábhoz rögzítjük, a másik végére egy elhanyagolható tömegű ütközőtányért erősítünk. Egy másik, $\displaystyle m$ tömegű test $\displaystyle v_0$ sebességgel nekicsúszik a tányérnak úgy, hogy az elegendő hosszúságú rugót részben összenyomja.

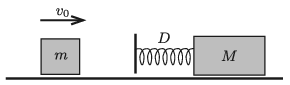
$\displaystyle a)$ Mekkora a rendszer tömegközéppontjának sebessége?

$\displaystyle b)$ A $\displaystyle m$ tömegű test és a tányér érintkezésétől számítva mennyi idő múlva lesz a rugó a legrövidebb?

Közli: Wiedemann László, Budapest

(5 pont)

A beküldési határidő 2020. március 10-én LEJÁRT.

I. megoldás. $\displaystyle a)$ A két testből álló rendszer össztömege $\displaystyle m+M$, összes lendülete $\displaystyle mv_0$, tehát a rendszer tömegközéppontjának sebessége

$\displaystyle v_\text{tkp}=\frac{m}{m+M}\,v_0.$

$\displaystyle b)$ A rugó összenyomódása (a ,,puha ütközés'') során a tömegközéppont sebessége mindvégig állandó marad, hiszen a rendszerre nem hat vízszintes irányú külső erő. A tömegközépponthoz rögzített vonatkoztatási rendszerben az $\displaystyle m$ tömegű test kezdősebessége

$\displaystyle v_m=v_0-v_\text{tkp}=\frac{M}{m+M}v_0,$

az $\displaystyle M$ tömegű hasáb kezdősebessége pedig

$\displaystyle v_M=0-v_\text{tkp}=-\frac{m}{m+M}v_0.$

(A sebességeket a kitűzési ábrán bejelölt (balról jobbra mutató) irányban tekintjük pozitívnak.) Nyilván fennáll, hogy $\displaystyle mv_m+Mv_M=0$, hiszen ebben a vonatkoztatási rendszerben a tömegközéppont nem mozog, az összes lendület tehát nulla.

Az ütközés során a rugónak az a pontja, amelyik az $\displaystyle m$ tömegű testhez $\displaystyle M/m$-szer közelebb van, mint a $\displaystyle M$ tömegű testtől mért távolsága, a rugó összenyomódása során mozdulatlan marad, tehát tekinthetjük akár rögzített pontnak. A rugót tehát gondolatban feloszthatjuk két részre, melyek rugóállandója $\displaystyle D_m$ és $\displaystyle D_M$, és ,,sorba vannak kapcsolva''. Ha az egész rugót $\displaystyle F$ erő nyomja, akkor a teljes összenyomódása $\displaystyle \Delta \ell=F/D.$ Ugyanakkor a $\displaystyle m$ tömegű testhez közelebbi rugódarab összenyomódása csak

$\displaystyle \Delta \ell_m= \frac{M}{m+M}\Delta \ell=F\, \frac{M}{D(m+M)}=\frac{F}{D_m}.$

Leolvashatjuk, hogy

$\displaystyle D_m=\frac{m+M}{M}D,$

és hasonló módon

$\displaystyle D_M=\frac{m+M}{m}D.$

Az ütközés úgy zajlik le, mintha az $\displaystyle m$ tömegű test egy rögzített végpontú, $\displaystyle D_m$ rugóállandójú rugót nyomna össze, illetve a $\displaystyle M$ tömegű test mozgását egy $\displaystyle D_M$ rugóállandójú rugó fékezi. Mindkét test rezgésidejének periódusideje

$\displaystyle T=2\pi\sqrt{\frac{m}{D_m}}=2\pi\sqrt{\frac{M}{D_M}}=2\pi\sqrt{\frac{mM}{m+M}\cdot \frac{1}{D}},$

a megállásukig (vagyis a rugó maximális összenyomódásáig)

$\displaystyle T_0=\frac{T}{4}= \frac{\pi}{2}\sqrt{\frac{mM}{m+M}\cdot \frac{1}{D}}$

idő telik el.

II. megoldás. Jelöljük a rugó összenyomódási szakaszában a testek pillanatnyi helyét $\displaystyle x_m$-mel és $\displaystyle x_M$-mel, a megfelelő pillanatnyi gyorsulásokat pedig $\displaystyle a_m$ és $\displaystyle a_M$ módon. A Newton-féle mozgásegyenletek:

$\displaystyle m\,a_m=-D\left(x_m-x_M\right),$

$\displaystyle M\,a_M=+D\left(x_m-x_M\right).$

Szorozzuk meg a első egyenletet $\displaystyle M$-mel, a másodikat $\displaystyle m$-mel, és vonjuk ki a két egyenletet egymásból:

$\displaystyle mM\left(a_m-a_M\right)=-D(m+M)\left(x_m-x_M\right).$

Látható, hogy a két test $\displaystyle a = a_m - a_M$ relatív gyorsulására és $\displaystyle x=x_m-x_M$ távolságára vonatkozó

$\displaystyle \frac{mM}{m+M}a=-Dx$

mozgásegyenlet ugyanolyan alakú, mint egyetlen, $\displaystyle D$ rugóállandójú rugó végén harmonikus rezgőmozgást végző $\displaystyle \frac{mM}{m+M}$ tömegű test mozgásegyenlete. A rugó összenyomódásának ideje tehát

$\displaystyle T_0=\frac{T}{4}= \frac{\pi}{2}\sqrt{\frac{mM}{m+M}\cdot \frac{1}{D}}.$

(Az $\displaystyle \frac{mM}{m+M}$ mennyiséget a két testből álló rendszer redukált tömegének nevezik.)

Statisztika:

27 dolgozat érkezett.
5 pontot kapott:	Békési Ábel, Bonifert Balázs, Fekete Levente, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Horváth 999 Anikó, Jánosik Áron, Kertész Balázs, Ludányi Levente, Nguyễn Đức Anh Quân, Somlán Gellért, Szabados Noémi, Szabó 314 László, Szász Levente, Téglás Panna, Viczián Anna.
4 pontot kapott:	Bokor Endre, Endrész Balázs, Hamar Dávid, Horváth 127 Ádám, Nagy 414 Soma, Selmi Bálint.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2020. februári fizika feladatai