 |
A P. 5232. feladat (2020. május) |
P. 5232. Vékony falú, celloidból készült keljfeljancsi alsó gömbjének sugara 3 cm. A játék belsejébe, alul egy 2 cm átmérőjű acélgolyót rögzítettek. A keljfeljancsit lassan kitérítjük úgy, hogy szimmetriatengelye a függőlegessel \(\displaystyle 30^\circ\)-os szöget zárjon be. Mekkora lesz a játék szögsebessége abban a pillanatban, amikor a tengelye átlendül a függőleges helyzeten? (A tapadó súrlódás elég nagy, a játék nem csúszik meg a talajon. A gördülő súrlódástól és a közegellenállástól eltekinthetünk.)
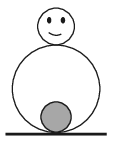
Közli: Kis Tamás, Heves
(4 pont)
A beküldési határidő 2020. június 10-én LEJÁRT.
Megoldás. Jelöljük az alsó gömb sugarát \(\displaystyle R\)-rel, az acélgolyó sugarát \(\displaystyle r\)-rel, a kitérítés szögét \(\displaystyle \alpha\)-val, a keresett szögsebességet pedig \(\displaystyle \omega\)-val. Az egyensúlyi helyzetben a helyzeti energia a kezdőállapot energiájánál
\(\displaystyle E_1=mg(R-r)(1-\cos\alpha)\)
értékkel kisebb. A rendszer (esetünkben az acélgolyó) mozgási energiája a függőleges tengelyű helyzetben a tömegközéppont körüli forgáshoz és a tömegközéppont haladó (transzlációs) mozgásához tartozó energia összege:
\(\displaystyle E_2=\frac{1}{2}\left(\frac{2}{5}mr^2\right)\omega^2 + \frac12 m(r\omega)^2=\frac{7}{10}mr^2\omega^2.\)
Ugyanezt az eredményt úgy is megkaphatjuk, hogy az acélgolyó forgási energiáját számítjuk ki, de nem a tömegközéppontra, hanem a talajjal érintkező pontjára vonatkoztatva. Erre a pontra a tehetetlenségi nyomaték (a Steiner-tétel szerint) \(\displaystyle \tfrac75mr^2\).
Az energiamegmaradás törvénye szerint \(\displaystyle E_1=E_2\), vagyis
\(\displaystyle \omega=\sqrt{\frac{10(R-r)g}{7r^2} (1-\cos\alpha) }=19{,}4~\frac{1}{\rm s}.\)
Statisztika:
31 dolgozat érkezett. 4 pontot kapott: Balázs 825 Ádám , Bonifert Balázs, Horváth Antal, Kozák Gergely, Somlán Gellért, Szabados Noémi, Szász Levente, Varga Vázsony. 3 pontot kapott: Bekes Barnabás, Bokor Endre, Dóra Márton, Endrész Balázs, Fiam Regina, Hamar Dávid, Kertész Balázs, Lê Minh Phúc, Mócza Tamás István, Németh Kristóf, Perényi Barnabás, Sas 202 Mór, Schäffer Bálint, Szabó 314 László, Téglás Panna. 1 pontot kapott: 8 versenyző.
A KöMaL 2020. májusi fizika feladatai
