A P. 5235. feladat (2020. május)

P. 5235. \(\displaystyle n=2\) mol anyagmennyiségű, egyatomos ideális gáz az ábrán látható \(\displaystyle A\to P\to B\) folyamatot végzi. A gáz hőmérséklete a kiinduló állapotban \(\displaystyle T_1=280~\)K, a végállapotban \(\displaystyle T_2=4T_1\). Az \(\displaystyle AP\) szakasz párhuzamos a \(\displaystyle V\) tengellyel, a \(\displaystyle BC\) szakasz meghosszabbítása átmegy az origón, a \(\displaystyle P\) pont pedig a \(\displaystyle BC\) szakasz felezőpontja.

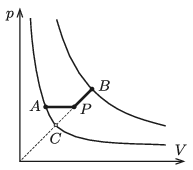
\(\displaystyle a)\) Határozzuk meg a gáz hőmérsékletét a \(\displaystyle P\) állapotban!

\(\displaystyle b)\) Mennyi hőt vesz fel a gáz az \(\displaystyle A\to P\to B\) folyamatban?

Közli: Kotek László, Pécs

(5 pont)

A beküldési határidő 2020. június 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) A gáztörvény szerint

\(\displaystyle pV=nRT.\)

Mivel \(\displaystyle T_2=4T_1\), a \(\displaystyle B\) állapotban a \(\displaystyle pV\) szorzat a \(\displaystyle C\) pontbelinek négyszerese. Másrészt a \(\displaystyle BC\) egyenes mentén \(\displaystyle p\) egyenesen arányos \(\displaystyle V\)-vel, így \(\displaystyle V_B=2V_C\) és \(\displaystyle p_B=2p_C\). Tudjuk, hogy a \(\displaystyle P\) pont a \(\displaystyle CB\) szakasz felezőpontja, tehát

\(\displaystyle V_P=\frac{3}{2}V_C, \qquad p_P=\frac{3}{2}p_C, \qquad \Rightarrow \qquad T_P=\frac{9}{4}T_C=630~\rm K.\)

\(\displaystyle b)\) Egyatomos ideális gáz moláris hőkapacitása állandó térfogaton

\(\displaystyle C_V=\frac{3}{2}R,\)

állandó nyomáson pedig

\(\displaystyle C_p=\frac{5}{2}R.\)

Az \(\displaystyle A\rightarrow P\) folyamat izobár, így a folyamat során felvett hő

\(\displaystyle Q_{AP}=\frac{5}{2}nR\left(T_P-T_A\right)=14{,}5~\rm kJ.\)

A felvett hő a belsőenergia-változás és a gáz által végzett munka összege. A \(\displaystyle P\rightarrow B\) folyamatban a belső energia változása:

\(\displaystyle \frac32nR(T_B - T_P) = 12{,}2~\rm kJ.\)

A munkavégzés:

\(\displaystyle \frac{p_P + p_B}{2} \cdot (V_B - V_P) = \frac78p_B \cdot \frac{1}{4}V_B =\frac7{32}p_B V_B = \frac7{32} nRT_B = 4{,}1~\rm kJ.\)

Tehát a hőközlés ezen a szakaszon:

\(\displaystyle Q_{PB} = 12{,}2~{\rm kJ} + 4{,}1~\rm kJ = 16{,}3~\rm kJ.\)

Megjegyzés. A fenti eredményt más úton is meg lehet kapni. A \(\displaystyle P\rightarrow B\) folyamat során

\(\displaystyle pV^{(-1)}=\text{állandó}.\)

Ez speciális esete a politropikus folyamatoknak, amelyben \(\displaystyle pV^\alpha=\text{állandó},\) és amelyek során a moláris hőkapacitás (lásd pl. a P. 5061. feladatot a KöMaL 2018. októberi számában):

\(\displaystyle C=\frac{C_p-\alpha C_V}{1-\alpha}.\)

Esetünkben az ún. politrop kitevő \(\displaystyle \alpha=-1\), így \(\displaystyle C=2R\), a felvett hő tehát:

\(\displaystyle Q_{PB}=2nR\left(T_B-T_P\right)=16{,}3~\rm kJ.\)

Az \(\displaystyle A\rightarrow P\rightarrow B\) folyamatban összesen felvett hő: 30,8 kJ.

Statisztika:

27 dolgozat érkezett.
5 pontot kapott:	Bekes Barnabás, Békési Ábel, Bokor Endre, Endrész Balázs, Györgyfalvai Fanni, Horváth 999 Anikó, Kertész Balázs, Ludányi Levente, Nguyễn Đức Anh Quân, Selmi Bálint, Somlán Gellért, Téglás Panna, Toronyi András, Varga Vázsony, Vass Bence, Viczián Anna.
4 pontot kapott:	Bonifert Balázs, Fekete András Albert, Fekete Levente, Schäffer Bálint, Tóth Ábel.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2020. májusi fizika feladatai