A P. 5247. feladat (2020. szeptember)

P. 5247. Egy téglatest alakú akvárium két szemközti oldalán egy-egy kör alakú nyílás van, melyeket vékony, kis nyílásszögű gömbsüvegek fednek (lásd az ábrát). A gömbsüvegek közös optikai tengelye vízszintes. A befelé domboruló gömbsüveg görbületi sugara \(\displaystyle r\), a kifelé domborulóé \(\displaystyle 2r\). A gömbsüvegek teteje alacsonyabban van, mint az akváriumban lévő, \(\displaystyle n=4/3\)-os törésmutatójú víz felszíne.

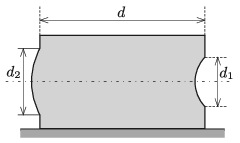
\(\displaystyle a)\) Mekkora \(\displaystyle d\) távolságra van egymástól az akvárium gömbsüvegeket tartalmazó két oldala, ha az egyik gömbsüvegre vízszintesen érkező, párhuzamos fénysugarak a másik gömbsüvegen át vízszintesen, párhuzamosan hagyják el az akváriumot?

\(\displaystyle b)\) Mekkora a két gömbsüveg \(\displaystyle d_2\), illetve \(\displaystyle d_1\) átmérőjének aránya, ha az akváriumba bármelyik gömbsüvegen át belépő, vízszintes fénynyaláb teljes egészében a másik gömbsüvegen lép ki?

\(\displaystyle c)\) Az optikai tengelyen, az akvárium közepén van egy piciny halacska. Hol látható ez az egyik, illetve a másik oldali gömbsüvegen át nézve?

Közli: Zsigri Ferenc, Budapest

(5 pont)

A beküldési határidő 2020. október 15-én LEJÁRT.

Megoldás. Ha \(\displaystyle n_1\) törésmutatójú közegben a tárgytávolság \(\displaystyle t\), \(\displaystyle n_2\) törésmutatójú közegben a képtávolság \(\displaystyle k\), és a két közeget \(\displaystyle R\) görbületi sugarú, gömbsüveg alakú felület választja el egymástól, akkor a leképezési törvény (lásd pl. a P. 5190. feladat megoldását a KöMaL 2020. évi 5. számának 309. oldalán, vagy a honlapon) így írható:

\(\displaystyle \frac{n_1}{t}+\frac{n_2}{k}=\frac{n_2-n_1}{R}.\)

(A képlet akkor érvényes, ha a gömbsüveg középpontja a kép oldalára esik.)

\(\displaystyle a)\) A levegőből párhuzamosan érkező, a kifele domborodó felületen keresztül a vízbe belépő fénynél \(\displaystyle n_1=1\), \(\displaystyle n_2=\tfrac43\), \(\displaystyle R=2r\) és \(\displaystyle t\) ,,végtelen nagy''. Ekkor a leképezési törvény szerint

\(\displaystyle 0+\frac{4/3}{k}=\frac{4/3-1}{2r},\)

ahonnan \(\displaystyle k=8r\) következik.

A vízből kilépő fényre \(\displaystyle n_1=\tfrac43\), \(\displaystyle n_2=1\), \(\displaystyle t=d-8r\), \(\displaystyle R=r\) és \(\displaystyle k\) ,,végtelen nagy''. A leképezési törvényből számolva

\(\displaystyle \frac{4/3}{d-8r}+0=\frac{1-4/3}{r},\)

innen az akvárium mérete: \(\displaystyle d=4 r\). A fénysugarak megfordíthatósága miatt ugyanezt az eredményt kapjuk, ha a fény az ellenkező oldalról érkezik.

\(\displaystyle b)\) A fenti számolás eredménye szerint a párhuzamosan érkező fénysugarak a kifelé domborodó gömbsüvegtől \(\displaystyle 8r\) távoli pont felé indulnak el, ami a befelé domborodó felülettől \(\displaystyle 4r\) távolságban van. Ezen távolságok aránya \(\displaystyle 2:1\), tehát a keresett \(\displaystyle d_2/d_1\) arány is 2. (Ez a görbült felületek legszélén áthaladó fénysugarak menetéből látszik.)

\(\displaystyle c)\) A halacska az akvárium közepén van, tehát \(\displaystyle t=2r\), továbbá \(\displaystyle n_1=\tfrac43\), illetve \(\displaystyle n_2=1\). A kifelé domborodó oldalról nézve \(\displaystyle R=-2r\) (a negatív előjel azt fejezi ki, hogy a gömbsüveg középpontja a tárgy oldalára esik). Ezek szerint

\(\displaystyle \frac{4/3}{2r}+\frac{1}{k}=\frac{1-4/3}{-2r},\)

tehát \(\displaystyle k=-2r\). A kép látszólagos, és a vízben, éppen a gömbsüveg görbületi középpontjánál jön létre.

A befelé domboruló oldalról nézve \(\displaystyle R=r\), vagyis

\(\displaystyle \frac{4/3}{2r}+\frac{1}{k}=\frac{1-4/3}{r},\)

ahonnan \(\displaystyle k=-r\) adódik. A kép most is látszólagos, és a vízben, a befelé domborodó gömbsüvegtől \(\displaystyle r\) távolságban jön létre.

Statisztika:

11 dolgozat érkezett.
5 pontot kapott:	Fekete András Albert, Kertész Balázs, Somlán Gellért, Tóth Ábel.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2020. szeptemberi fizika feladatai