 Problem P. 5264. (November 2020)
Problem P. 5264. (November 2020)
P. 5264. A racing car starts from rest and goes along a circular race track of radius 60 m. Its tangential acceleration is constant in the first four seconds of its motion, its magnitude is \(\displaystyle 6~\mathrm{m/s}^2\).
\(\displaystyle a)\) Determine the angular speed at which the acceleration vector rotates with respect to the direction of the motion of the car. Sketch this angular speed as a function of the time.
\(\displaystyle b)\) How much time elapses until this angular speed becomes the greatest? What is this greatest angular speed?
(5 pont)
Deadline expired on December 15, 2020.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. \(\displaystyle a)\) SI-egységeket használva:
– az autó érintőleges gyorsulása \(\displaystyle a_1=6\);
– a pálya sugara: \(\displaystyle r=60\);
– az autó sebessége \(\displaystyle t\) idő elteltével \(\displaystyle v=a_1t=6t\);
– az autó centripetális gyorsulása: \(\displaystyle a_2=\frac{v^2}{r}=0{,}6\,t^2\). Az autó gyorsulásvektora a kör érintőjével
\(\displaystyle \alpha(t)=\arctg\frac{a_2}{a_1}=\arctg(0{,}1\,t^2)\)
szöget zár be. Ennek a szögnek az egységnyi időre vonatkozó megváltozása a keresett
\(\displaystyle \omega(t)= \frac{\Delta\alpha}{\Delta t} \)
szögsebesség.
Számítsuk ki, hogy mennyit változik \(\displaystyle \tg\alpha\) egy kicsiny \(\displaystyle \Delta t\) idő alatt, ha eközben az \(\displaystyle \alpha\) szög \(\displaystyle \Delta\alpha\)-val nagyobb lesz. Mivel \(\displaystyle \tg\alpha=0{,}1\,t^2\), fennáll, hogy
\(\displaystyle \tg(\alpha+\Delta\alpha)-\tg\alpha=0{,}1 (t+\Delta t)^2-0{,}1 t^2.\)
Kicsiny változások esetén érvényes
\(\displaystyle \tg(\Delta\alpha)\approx \Delta\alpha\qquad \text{és}\qquad \Delta t\ll t.\)
Trigonometriai és algebrai átalakítások után kapjuk, hogy ebben a közelítésben
\(\displaystyle \frac{\tg\alpha+\Delta\alpha}{1-\Delta\alpha\cdot \tg\alpha}-\tg\alpha=0{,}2t\,\Delta t+0{,}1(\Delta t)^2,\)
azaz
\(\displaystyle \Delta\alpha\left(1+\tg^2\alpha\right)=\Delta t(0{,}2t+0{,}1t\,\Delta t)(1-\Delta\alpha\,\tg\alpha).\)
Innen kapjuk, hogy a keresett szögsebesség:
\(\displaystyle \omega(t)\approx \frac{\Delta\alpha}{\Delta t}= \frac{0{,}2\,t+0{,}1\Delta t}{1+\tg^2\alpha} (1-\Delta\alpha\cdot\tg\alpha) =\frac{0{,}2\,t}{1+0{,}01\,t^4}.\)
Ha ábrázoljuk az \(\displaystyle \omega(t)\) függvényt, a grafikonról leolvashatjuk, hogy a szögsebességnek \(\displaystyle t=2{,}4\) s közelében maximuma van, és hogy a szögsebesség legnagyobb értéke \(\displaystyle \omega_\text{max}=0{,}36\, \rm s^{-1}\).
Megjegytés. \(\displaystyle \omega(t)\) szélsőértékét deriválással is meghatározhatjuk: A differenciálhányados \(\displaystyle t_0=\sqrt[4]{100/3} \approx 2{,}4\ {\rm s}\) idő elteltével lesz nulla, és \(\displaystyle \omega_\text{max}=\omega(t_0)\approx 0{,}36\,\rm s^{-1}\).
II. megoldás. A feladat elemi úton (a differenciálszámítás felhasználása nélkül) is megoldható. Az autó inerciarendszerbeli \(\displaystyle \boldsymbol a\) gyorsulásvektora az autóhoz rögzített (tehát egyenletes gyorsuló szögsebességgel forgó) \(\displaystyle (X,Y)\) koordináta-rendszerben \(\displaystyle \boldsymbol a=(a_1, a_2)\) módon adható meg (1. ábra), ahol – az I. megoldás elején leírtaknak megfelelően
\(\displaystyle a_1= 6 \qquad \text{és}\qquad a_2=0{,}6\,t^2.\)
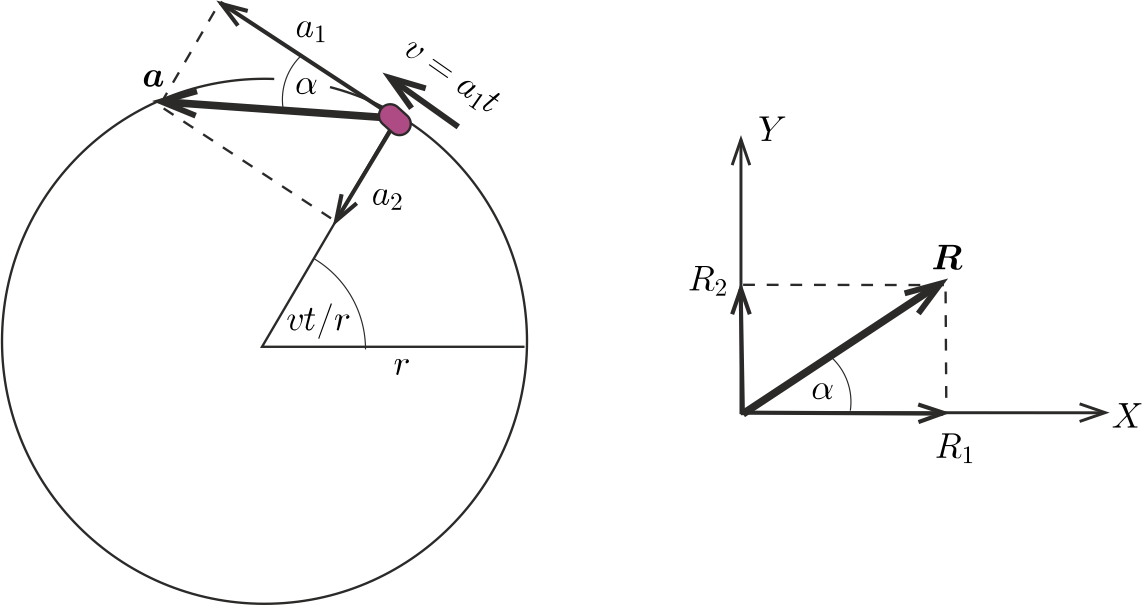
1. ábra
A továbbiakban a gyorsulásvektort \(\displaystyle \boldsymbol R\)-rel, ezen vektor változási sebességét \(\displaystyle \boldsymbol V\)-rel, ez utóbbi változási sebességét (vagyis a \(\displaystyle \boldsymbol R\) gyorsulását) \(\displaystyle \boldsymbol A\)-val fogjuk jelölni. (Az átjelölés oka: el akarjuk kerülni a \(\displaystyle \boldsymbol V\) vektornak és az autó \(\displaystyle \boldsymbol v\) sebességvektorának, valamint \(\displaystyle \boldsymbol A\)-nak és \(\displaystyle \boldsymbol a\)-nak esetleges összetévesztését.) Ennek megfelelően írhatjuk, hogy
\(\displaystyle R_1= 6, \qquad R_2=0{,}6\,t^2.\)
Ráismerhetünk, hogy ezek éppen egy olyan test koordinátái, amely az \(\displaystyle Y\) tengely irányában egyenletesen gyorsuló mozgást végez \(\displaystyle 1{,}2\) nagyságú gyorsulással. Így tehát
\(\displaystyle V_1= 0, \qquad V_2=1{,}2\,t,\)
és
\(\displaystyle A_1= 0, \qquad A_2=1{,}2.\)
Az \(\displaystyle \boldsymbol R\) vektor nagyságát jelölje \(\displaystyle R\), az autó haladási irányával (vagyis az \(\displaystyle X\) tengellyel) bezárt szöge pedig legyen \(\displaystyle \alpha\). Ennek megfelelően
| \(\displaystyle (1)\) | \(\displaystyle R=\sqrt{R_1^2+R_2^2}=6\sqrt{1+0{,}01\,t^4},\) |
továbbá
| \(\displaystyle (2)\) | \(\displaystyle \cos\alpha=\frac{R_1}{R}=\frac{1}{\sqrt{1+0{,}01\,t^4}}\) |
és
\(\displaystyle \sin\alpha=\frac{R_2}{R}=\frac{0{,}1\,t^2}{\sqrt{1+0{,}01\,t^4}.} \)
a) A \(\displaystyle \boldsymbol V\) vektort nemcsak az \(\displaystyle X,Y\) koordinátákkal, hanem \(\displaystyle \boldsymbol R\) irányú \(\displaystyle V_\text{rad}\) ,,radiális'' és arra merőleges \(\displaystyle V_\text{tan}\) ,,tangenciális'' komponensekkel is jellemezhetjük (2. ábra).
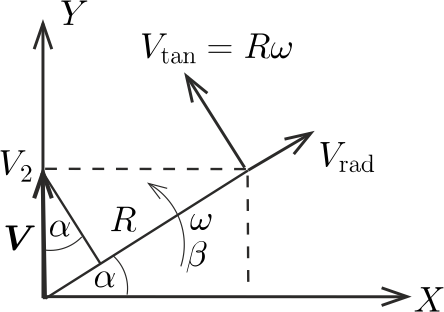
2. ábra
Az ábráról leolvashatjuk, hogy
\(\displaystyle V_\text{rad}=V_2\sin\alpha={1{,}2\,t}\, \frac{0{,}1\,t^2}{\sqrt{1+0{,}01\,t^4}}=\frac{0{,}12\,t^3}{\sqrt{1+0{,}01\,t^4}},\)
valamint
| \(\displaystyle (3)\) | \(\displaystyle V_\text{tan}=R\omega=V_2\cos\alpha=\frac{1{,}2\,t }{\sqrt{1+0{,}01\,t^4}},\) |
tehát a kérdéses szögsebesség:
| \(\displaystyle (4)\) | \(\displaystyle \omega=\frac{V_\text{tan}}{R}=\frac{0{,}2\,t }{ 1+0{,}01\,t^4} .\) |
b) A fentebb leírtakhoz hasonlóan járhatunk el az \(\displaystyle \boldsymbol A\) vektorral is (3. ábra).
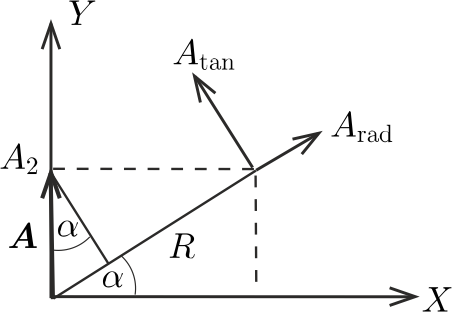
3. ábra
Itt azonban figyelembe kell vegyük, hogy a radiális és a tangenciális komponensek, valamint az \(\displaystyle (A_1,A_2)\) komponensek közötti kapcsolat a forgásból származó extra tagokat is tartalmaz:
\(\displaystyle A_\text{rad}= \frac{\Delta V_\text{rad}}{\Delta t}-R\omega^2, \)
ahol a jobb oldal második tagja a centripetális gyorsulás, valamint
| \(\displaystyle (5)\) | \(\displaystyle A_\text{tan}=R\beta+2V_\text{rad}\,\omega, \) |
ahol a jobb oldal második tagja a Coriolis-gyorsulás.
Megjegyzás. Egy \(\displaystyle m\) tömegű test forgó koordináta-rendszerbeli mozgásegyenletében a centrifugális erő a centripetális gyorsulás \(\displaystyle (-m)\)-szerese, a Coriolis-erő pedig a Coriolis-gyorsulás \(\displaystyle (-m)\)-szerese. (Lásd pl. a Négyjegyű függvénytáblázatokban a tehetetlenségi erők képleteit.)
Abban a \(\displaystyle t_0\) pillanatban, amikor az \(\displaystyle \omega\) szögsebesség a legnagyobb, a \(\displaystyle \beta\) szöggyorsulás nulla, így (1-5) egyenletekből következően
\(\displaystyle A_2\,\cos\alpha=2V_\text{rad}\,\omega,\)
azaz
\(\displaystyle {1{,}2}\cdot\frac{1}{\sqrt{1+0{,}01\,t_0^4}}=2\cdot\frac{0{,}12\,t_0^3}{\sqrt{1+0{,}01\,t_0^4}}\cdot\frac{0{,}2\,t_0 }{\ 1+0{,}01\,t_0^4} .\)
Innen
\(\displaystyle 0{,}04\,t_0^4=1+0{,}01\,t_0^4,\qquad \text{azaz}\qquad t_0=\root 4 \of {\frac{1}{0{,03}}}\approx 2{,}4\ \rm [s], \)
a szögesbesség legnagyobb értéke pedig
\(\displaystyle \omega_\text{max}=\omega(t_0)=\frac{3}{20}\root 4 \of {\frac{100}{3}}\approx 0{,}36\ \left[\rm s^{-1}\right].\)
Statistics:
40 students sent a solution. 5 points: Bonifert Balázs, Fekete András Albert, Fey Dávid, Fonyi Máté Sándor, Gurzó József, Horváth 999 Anikó, Jánosik Máté, Juhász Márk Hunor, Kertész Balázs, Kovács Kinga, Ludányi Levente, Molnár-Szabó Vilmos, Németh Kristóf, Sas 202 Mór, Schäffer Bálint, Selmi Bálint, Simon László Bence, Somlán Gellért, Takács Bendegúz, Téglás Panna, Tóth Ábel, Varga Vázsony. 4 points: Koleszár Benedek, Köpenczei Csanád, Magyar Gábor Balázs, Mihalik Bálint, Molnár 123 Barnabás, Toronyi András. 2 points: 8 students. 1 point: 2 students. 0 point: 2 students.
Problems in Physics of KöMaL, November 2020
