A P. 5295. feladat (2021. február)

P. 5295. Egy LEGO-motorral hajtott $\displaystyle m$ tömegű kisautó $\displaystyle \alpha$ hajlásszögű lejtőn felfelé indul el. A motor mechanikai teljesítménye (az indulás utáni nagyon rövid időtartamot leszámítva) állandó $\displaystyle P$ értékű. Mekkora lesz a végsebessége? (A kerekek nem csúsznak, és a gördülő ellenállás elhanyagolhatóan kicsi.)

$\displaystyle a)$ Írjuk le, milyen jellegű a kisautó mozgása!

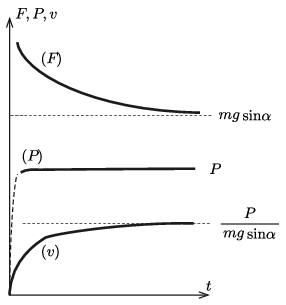
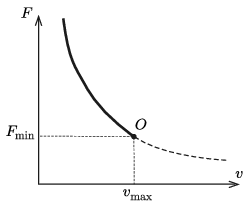
$\displaystyle b)$ Ábrázoljuk vázlatosan egy közös diagramon a teljesítményt, a sebességet, valamint a kerekekre ható tapadási súrlódási erőt az idő függvényében! Készítsük el az erő–sebesség grafikont is!

$\displaystyle c)$ Mekkora a mozgás során a legkisebb súrlódási erő?

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2021. március 16-án LEJÁRT.

Megoldás. Az $\displaystyle F\cdot v=P$ összefüggésből indulunk ki, ahol a $\displaystyle F$ a kisautó vonóerejét, $\displaystyle v$ a sebességet jelenti. Ez az egyenlőség a mozgás során minden pillanatban fennáll, így pl. ha $\displaystyle v$ időbeli változását ismerjük, ennek segítségével $\displaystyle F$ változása azonnal megállapítható. Az $\displaystyle m$ tömegű kisautó $\displaystyle a$ gyorsulása:

$\displaystyle a=\frac{F-mg\sin\alpha}{m}= \frac{P}{mv}- g\sin\alpha .$

Ennek az összefüggésnek a segítségével már végigkövethetjük a mozgást. Kezdetben $\displaystyle v$ még kicsi, így $\displaystyle F$ igen nagy, a kisautó nagy gyorsulással indul. (Természetesen $\displaystyle F$ végtelen értékének nem tulajdoníthatunk realitást. Itt arról van szó, hogy a motor teljesítménye az induláskor $\displaystyle 0$-ról nagyon gyorsan, elhanyagolhatóan rövid idő alatt növekszik a $\displaystyle P$ értékre, és a továbbiakban konstans marad.) Ahogy a kisautó sebessége nő, úgy csökken a fenti képlet szerint az autó gyorsulása, tehát a sebesség a kezdeti rohamos növekedés után egyre lassabban növekszik. Ez a növekedés a

$\displaystyle v_\text{max}=\frac{P}{mg\sin\alpha}$

értékig tarthat, ekkor ugyanis a gyorsulás nullává válik, így a sebesség ezután már nem változna. Bebizonyítható, hogy ezt az értéket a kisautó csak ,,végtelen hosszú idő múlva'' érné el, aszimptotikusan közelíti meg azt (1. ábra).

1. ábra

Az erő-sebesség grafikon (2. ábra) a $\displaystyle F\cdot v=P$ összefüggésnek megfelelően hiperbola alakú, amely a $\displaystyle v=v_\text{max}$-nak megfelelő $\displaystyle O$ pontnál véget ér. Az erő a minimális értékét itt éri el (a megbeszélt értelemben ,,végtelen'' idő múlva):

$\displaystyle F_{\text{min}}=mg\sin\alpha.$

Ekkora erő nyilván kell a lejtőn való visszacsúszás megakadályozására. A hiperbola szaggatottan jelölt részébe soha nem juthatunk el, az ezeknek megfelelő állapotok nem valósulnak meg.

2. ábra

Statisztika:

21 dolgozat érkezett.
5 pontot kapott:	Albert Máté, Bonifert Balázs, Dóra Márton, Fonyi Máté Sándor, Gurzó József, Ludányi Levente, Ruzsa Bence, Varga Vázsony.
4 pontot kapott:	Gábriel Tamás, Hauber Henrik, Köpenczei Csanád.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2021. februári fizika feladatai