 Problem P. 5297. (February 2021)
Problem P. 5297. (February 2021)
P. 5297. The length of a light, flexible but unstretchable fishing line is \(\displaystyle \ell=80\) cm. The two ends of the fishing line are fixed at two points at the same height, at a certain distance of each other. A steel marble of mass \(\displaystyle m=5\) g, which has a hole drilled through it, can slide along the fishing line. This bead is started from a position such that one part of the tight fishing line is vertical.
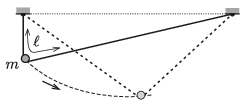
\(\displaystyle a)\) To what maximum speed can the steel marble speed up, if friction and air drag are negligible?
\(\displaystyle b)\) What is the tension in the fishing line when the speed of the steel marble is maximum?
(5 pont)
Deadline expired on March 16, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A golyó pályája (a damil hosszának állandósága miatt) egy olyan ellipszis, amelynek fél nagytengelye \(\displaystyle a= 40~\rm cm\) hosszúságú, és a fókuszpontjai a damilszál rögzítési pontjai. A fókuszpontok távolságát \(\displaystyle 2c\)-vel jelölve az ellipszis fél kistengelye \(\displaystyle b=\sqrt{a^2-c^2}\). A lecsúszó test sebessége akkor lesz a legnagyobb, amikor a kezdeti helyzetéhez képest a legnagyobb a függőleges irányú lesüllyedése. Ez a helyzet az ellipszis kistengelyének alsó végpontja.
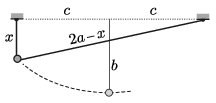
\(\displaystyle a)\) Kezdetben az acélgolyó a nagytengely alatt, attól \(\displaystyle x \) távolságra van. Az ábrán látható derékszögű háromszögre felírt Pitagorasz-tételből leolvashatjuk, hogy
\(\displaystyle x^2+(2c)^2=(2a-x)^2,\)
innen
\(\displaystyle x=\frac{a^2-c^2}{a}=\frac{b^2}{a}.\)
A pálya legmélyebb pontjánál a test távolsága a nagytengelytől \(\displaystyle b\), tehát a munkatétel szerint
\(\displaystyle \frac{1}{2}mv_\text{max}^2=mg\left(b-\frac{b^2}{a}\right),\)
ahonnan
\(\displaystyle v_\text{max}=\sqrt{2g\left(b-\frac{b^2}{a}\right)}.\)
Mivel \(\displaystyle g\) és \(\displaystyle a\) adott nagyságú, a zárójelben álló, \(\displaystyle b\)-től kvadratikusan függő kifejezés akkor lesz a legnagyobb, amikor a \(\displaystyle b=a/2\). Innen már következik, hogy
\(\displaystyle v_\text{max}=\sqrt{\frac{ga}{2}}=1{,}4~\frac{\rm m}{\rm s}.\)
\(\displaystyle b)\) A kistengely végpontjánál az ellipszis görbületi sugara: \(\displaystyle R=a^2/b\), esetünkben \(\displaystyle R=2a\). Ha a damilt az acélgolyó legnagyobb sebességénél \(\displaystyle F\) erő feszíti, akkor a két oldalon ható erők eredője függőlegesen felfelé mutat, és a nagysága \(\displaystyle b=a/2\) miatt ugyancsak \(\displaystyle F\). A mozgásegyenlet szerint
\(\displaystyle F-mg=m\frac{v_\text{max}^2}{R},\)
ahonnan a keresett erő:
\(\displaystyle F=mg+m\frac{v_\text{max}^2}{R}=mg+m\frac{ga}{2\cdot 2a}=\frac 54 mg\approx 0{,}06~\rm N.\)
Statistics:
41 students sent a solution. 5 points: Antalóczy Szabolcs, Bonifert Balázs, Fonyi Máté Sándor, Hauber Henrik, Kertész Balázs, Ludányi Levente, Mozolai Bende Bruno, Németh Kristóf, Sas 202 Mór, Selmi Bálint, Somlán Gellért, Téglás Panna, Toronyi András, Tóth Ábel, Varga Vázsony, Viczián Máté. 4 points: Biebel Botond, Fekete András Albert, Gábriel Tamás, Köpenczei Csanád, Páhán Anita Dalma, Puskás Attila, Schmercz Blanka. 3 points: 6 students. 2 points: 3 students. 1 point: 5 students. 0 point: 3 students. Unfair, not evaluated: 1 solutions.
Problems in Physics of KöMaL, February 2021
