 |
A P. 5334. feladat (2021. május) |
P. 5334. A fizikai kísérletezést kedvelő Rudi születésnapjára elektronikai készletet kapott. Tüstént össze is állította az ábra szerinti kapcsolást, melyben az \(\displaystyle U = 30\) V feszültségű áramforrás belső ellenállása elhanyagolható, a teljesen egyforma feszültségmérők és a teljesen egyforma árammérők pedig ideálisnak tekinthetők. Az ellenállások nagysága \(\displaystyle R = 50~\Omega\).
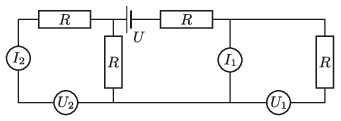
\(\displaystyle a)\) Mennyit mutattak a műszerek?
\(\displaystyle b)\) Majd megcserélte az 1-es árammérőt az 1-es feszültségmérővel, a 2-es árammérőt a 2-es feszültségmérővel. Mennyit mutattak így a műszerek?
\(\displaystyle c)\) Ezt követően visszarendezte a mérőműszereket az eredeti helyükre, majd az 1-es árammérőt és a 2-es feszültségmérőt felcserélte egymással. Mennyit mutattak így a műszerek?
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2021. június 15-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Az ideális árammérő rövidzárnak, az ideális feszültségmérő pedig szakadásnak felel meg, tehát a kapcsolás az eredeti elrendezésben az 1. ábrán láthatónak felel meg.
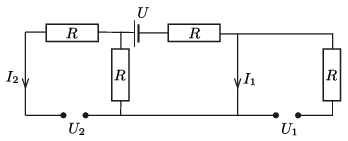
1. ábra
Az ábráról leolvashatjuk, hogy
\(\displaystyle I_1=\frac{U}{2R}=0{,}3~{\rm A}\qquad \text{és}\qquad U_1=0,\qquad U_2=I_1R=\frac{U}{2}=15~{\rm V} ,\qquad I_2=0.\)
\(\displaystyle b)\) A műszerek felcserélése után kialakuló kapcsolás a (2. ábrán) látható.
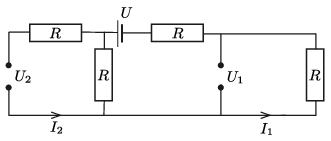
2. ábra
Látjuk, hogy
\(\displaystyle I_2=0,\qquad I_1=\frac{U}{3R}=0{,}2~{\rm A},\qquad U_1=U_2=I_1R=\frac{U}{3}=10~{\rm V}.\)
\(\displaystyle c)\) A kapcsolás ekkor a 3. ábrának megfelelő:
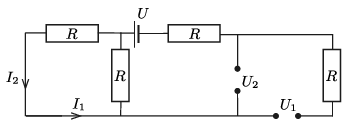
3. ábra
Ennek megfelelően
\(\displaystyle I_1=I_2=0, \qquad U_1=U_2=U=30~{\rm V}. \qquad \)
Statisztika:
25 dolgozat érkezett. 5 pontot kapott: Antalóczy Szabolcs, Beke Bálint, Biebel Botond, Bonifert Balázs, Hauber Henrik, Horváth 999 Anikó, Juhász Márk Hunor, Kertész Balázs, Ludányi Levente, Mozolai Bende Bruno, Páhán Anita Dalma, Somlán Gellért, Téglás Panna, Toronyi András, Török 111 László, Varga Vázsony. 4 pontot kapott: Fekete András Albert, Horváth 221 Zsóka, Köpenczei Csanád, Mócza Tamás István, Schmercz Blanka. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2021. májusi fizika feladatai

