A P. 5346. feladat (2021. október)

P. 5346. Vízszintes talajon egyenletesen haladunk egy nagy kerekű, $\displaystyle G=100$ N súlyú talicskával. Ekkor 25-25 N erőt kell kifejtenünk függőlegesen a talicska rúdjainak a végére. Vonalzóval és szögmérővel történő szerkesztéssel határozzuk meg, hogy mekkora és milyen irányú $\displaystyle \boldsymbol F$ erőt kell kifejtenünk a rudak végére, ha ugyanezzel a talicskával $\displaystyle \alpha=18^\circ$-os lejtőn haladunk felfelé, illetve lefelé! Igazoljuk számítással is a szerkesztés eredményét! Az egyszerűség kedvéért tegyük fel, hogy a rudak végének a távolsága a talajtól minden esetben megegyezik a talicska kerekének sugarával, és a talicska súlypontja is ugyanekkora távolságra van a talajtól.

Közli: Honyek Gyula, Veresegyház

(4 pont)

A beküldési határidő 2021. november 15-én LEJÁRT.

Megoldás. A vízszintes helyzetben kifejtett erőből látszik, hogy a talicska súlypontja éppen a kerék és a rudak vége között középen, mindkettőtől ugyanakkora ($\displaystyle \ell$) távolságra van.

Készítsünk olyan ábrát, amelyen az $\displaystyle \alpha$ szöget szögmérővel kimért $\displaystyle 18^\circ$-ra állítjuk be (1. ábra). A talicska méretét a rajzon önkényesen választhatjuk meg.

Tudjuk, hogy a súlyerő hatásvonala a $\displaystyle T$ tömegközépponton átmenő függőleges egyenes. Azt is tudjuk, hogy a keréknél a lejtő irányára merőleges erő hat (ellenkező esetben a kerékre ható eredő forgatónyomaték nem lenne nulla). A kerékre ható $\displaystyle \boldsymbol N$ nyomóerő nagyságát nem ismerjük, csak azt tudjuk, hogy a hatásvonala átmegy az $\displaystyle A$ ponton (a kerék tengelyén). A súlyerő és a nyomóerő hatásvonala a $\displaystyle P$ pontban metszi egymást, és ugyanezen a pontok kell áthaladnia a $\displaystyle B$ pontban kifejtett, ismeretlen nagyságú $\displaystyle \boldsymbol F$ erőnek is.

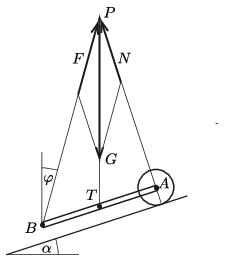
1. ábra

A $\displaystyle P$ pontig eltolt $\displaystyle \boldsymbol F$ és $\displaystyle \boldsymbol N$ vektor összege $\displaystyle -\boldsymbol G$-t kell adjon. Az ábráról vonalzóval és szögmérővel leolvashatjuk, hogy az erők nagyságával arányos $\displaystyle F$ és $\displaystyle G$ távolságok aránya kb. 0,57, vagyis $\displaystyle F\approx 57~$N, és a függőlegessel bezárt $\displaystyle \varphi$ szög kb. $\displaystyle 15^\circ$. A talicska száraira tehát egyenként kb. 28,5 N erőt kell kifejteni, és azok a függőlegestől $\displaystyle 15^\circ$-kal ,,előrefelé'' dőlnek.

Hasonló módon végezhetjük el a szerkesztést a lefelé haladó talicskánál is (2. ábra).

2. ábra

Az ábráról leolvashatjuk, hogy $\displaystyle F$ nagysága itt is kb. 57 N, és a függőlegessel bezárt szöge ugyancsak kb. $\displaystyle 15^\circ$, de most a rudak végénél kifejtett erő ,,hátrafelé'' dől.

A kétféle elrendezés azonos végeredménye nem véletlen. Ha ugyanis az 1. ábrán látható talicska erőrendszerét a $\displaystyle T$ ponton átmenő és az ábra síkjára merőleges tengely körül $\displaystyle 180^\circ$-kal elforgatjuk, majd mindhárom erő irányát megfordítjuk, akkor éppen a 2. ábra erőrendszerét kapjuk.

A szerkesztéssel kapott eredményt számítással is ellenőrizhetjük, pontosíthatjuk. A 3. ábrán látható jelöléseket fogjuk használni.

3. ábra

A $\displaystyle PAB$ derékszögű háromszögből leolvashatjuk, hogy $\displaystyle AP=2\ell \tg\beta$, a $\displaystyle PAT$ derékszögű háromszögből pedig azt, hogy $\displaystyle AP=\frac{\ell}{ \tg\alpha}$. Ezek szerint

$\displaystyle \tg\beta=\frac{1}{2\tg\alpha}=\frac{1}{2\tg18^\circ}=1{,}539 \qquad \Rightarrow \qquad \beta=56{,}98^\circ\approx 57^\circ.$

A talicska rúdjainak végénél összesen kifejtett $\displaystyle \boldsymbol F$ erőnek a függőlegessel bezárt szöge

$\displaystyle \varphi=90^\circ-(\alpha+\beta)=15{,}02^\circ\approx 15^\circ.$

Felírhatjuk meg a $\displaystyle PSR$ háromszögre a szinusztételt:

$\displaystyle \frac{\vert\boldsymbol F\vert}{\vert\boldsymbol G\vert}=\frac{PR}{PQ}=\frac{\sin\alpha}{\sin(90^\circ+\beta)}=0{,}567.$

Ezek szerint a rúdvégekre összesen $\displaystyle 56{,}7~{\rm N}\approx 57~{\rm N}$ erőt kell kifejtenünk.

Statisztika:

26 dolgozat érkezett.
4 pontot kapott:	Albert Máté, Gábriel Tamás, Horváth 221 Zsóka, Mészáros Ádám, Murai Dóra Eszter, Schmercz Blanka, Visontai Barnabás Péter.
3 pontot kapott:	Fajszi Karsa, Kovács Kinga, Köpenczei Csanád, Marozsi Lenke Sára, Nagy 456 Imre, Vágó Botond, Waldhauser Miklós.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2021. októberi fizika feladatai