 |
A P. 5402. feladat (2022. április) |
P. 5402. Egy \(\displaystyle R\) sugarú, elhanyagolható tömegű, vékony hengeres abroncsra egy \(\displaystyle m\) tömegű, pontszerű nehezéket erősítettünk. Az abroncs az ábrán látható labilis egyensúlyi helyzetéből kimozdul, és akkor csúszik meg a talajon, amikor középpontjának elmozdulása éppen \(\displaystyle R\). Mekkora a tapadási súrlódási együttható az abroncs és a vízszintes talaj között?
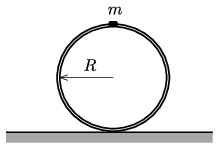
Közli: Balogh Péter, Gödöllő
(5 pont)
A beküldési határidő 2022. május 16-án LEJÁRT.
I. megoldás. Az abroncsot és a pontszerű nehezéket tekinthetjük egyetlen merev testnek, amelynek tömegközéppontja a nehezéknél van, így a tömegközéppontra vonatkoztatott tehetetlenségi nyomatéka elhanyagolhatóan kicsi, nullának tekinthető. A megcsúszás pillanatában az abroncs középpontjának elmozdulása \(\displaystyle R\), az abroncs elfordulása tehát az ábrának megfelelően
\(\displaystyle \alpha=1\ \text{radián}=57{,}3^\circ.\)
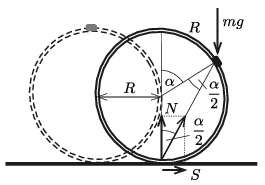
1. ábra
A talajnál ható \(\displaystyle N\) nyomóerő és \(\displaystyle S\) súrlódási erő eredője a tömegközéppont, vagyis a nehezék irányába mutat, hiszen a rendszer tehetetlenségi nyomatéka erre a pontra vonatkoztatva nulla. Az ábráról leolvashatjuk, hogy a tapadási súrlódási együttható
\(\displaystyle \mu_0=\frac{S}{N}={\rm tg}\,\frac{\alpha}{2}\approx 0{,}55.\)
II. megoldás. Az \(\displaystyle \alpha=1\) radián szöggel elfordult helyzetben az abroncs és a hozzá erősített nehezék a \(\displaystyle P\) ponton átmenő, a szimmetriatengellyel párhuzamos egyenes (az ún. pillanatnyi forgástengely) körül fordul el, így a nehezék \(\displaystyle \boldsymbol v\) sebességvektora merőleges a \(\displaystyle PQ\) egyenesre.
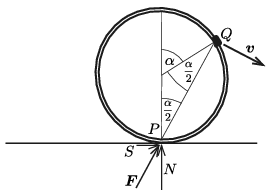
2. ábra
Másrészt tudjuk, hogy a talaj által kifejtett \(\displaystyle \boldsymbol F\) erő (ami a karika közvetítésével a nehezékre ható kényszererővel egyezik meg) nem végez munkát, emiatt \(\displaystyle \boldsymbol F\) merőleges \(\displaystyle \boldsymbol v\)-re, vagyis \(\displaystyle PQ\) irányú. Fennáll tehát, hogy
\(\displaystyle \mu_0=\frac{S}{N}={\rm tg}\,\frac{\alpha}{2}\approx 0{,}55.\)
Statisztika:
23 dolgozat érkezett. 5 pontot kapott: Beke Bálint, Bencz Benedek, Dóra Márton, Kertész Balázs, Nemeskéri Dániel, Toronyi András. 4 pontot kapott: Somlán Gellért, Téglás Panna. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2022. áprilisi fizika feladatai
