A P. 5405. feladat (2022. április)

P. 5405. Két különálló ellenálláson összesen $\displaystyle I$ erősségű áram folyik át. Igazoljuk, hogy a két ellenállásra eső összteljesítmény akkor minimális, ha a két ellenállásra eső feszültség megegyezik!

Közli: Holics László, Budapest

(4 pont)

A beküldési határidő 2022. május 16-án LEJÁRT.

I. megoldás. Legyen az $\displaystyle R_1$ ellenálláson átfolyó áram erőssége $\displaystyle I_1=x$, az $\displaystyle R_2$ ellenálláson folyó áram erőssége pedig $\displaystyle I_2=I-x$. A két ellenállásra jutó összteljesítmény (ami nyilván $\displaystyle x$ függvénye):

$\displaystyle P(x)=I_1^2R_1+I_2^2R_2=R_1x^2+R_2(I-x)^2=(R_1+R_2)x^2-2R_2I\,x+I^2R_2.$

Ezt a kifejezést teljes négyzetté alakítva leolvashatjuk, hogy

$\displaystyle P(x)=(R_1+R_2)\left(x-\frac{R_2 }{R_1+R_2 }I \right)^2+\frac{R_1R_2}{R_1+R_2}\,I^2$

akkor a legkisebb, amikor

$\displaystyle x=I_1=\frac{R_2 }{R_1+R_2}I,$

és ugyanekkor

$\displaystyle I_2=I-I_1=\frac{R_1}{R_1+R_2}I.$

Látható, hogy $\displaystyle I_1R_1=I_2R_2$, vagyis az ellenállásokra eső feszültségek valóban megegyeznek.

Az összeteljesítmény legkisebb értéke:

$\displaystyle P_\text{min}=\frac{R_1R_2}{R_1+R_2}\,I^2.$

II. megoldás. Legyen $\displaystyle I_1\sqrt{R_1} \equiv x_1$ és $\displaystyle I_2\sqrt{R_2} \equiv x_2$. Az összteljesítmény ezekkel a változókkal:

az áramok összegének állandósága pedig így írható fel:

Az (1) összefüggés az $\displaystyle (x_1,x_2)$ koordináta-rendszerben egy $\displaystyle \sqrt P$ sugarú kör egyenlete, (2) pedig egy olyan egyenest határoz meg, aminek tengelymetszetei $\displaystyle I\sqrt{R_1}$ és $\displaystyle I\sqrt{R_2}$ (lásd az ábrát).

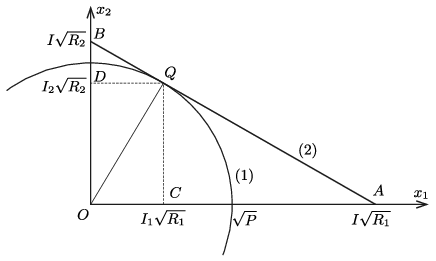
A legkisebb összteljesítmény annak a körnek felel meg, amelyiknek egyetlen közös pontja a (2) egyenessel, vagyis amelyik érinti az egyenest. Ebben az esetben $\displaystyle OQ$ merőleges $\displaystyle AB$-re, és így az $\displaystyle OCQ$ és $\displaystyle BOA$ háromszögek hasonlóak. Ennek megfelelően fennáll

$\displaystyle \frac{OC}{OD}=\frac{I_1\sqrt{R_1}}{I_2\sqrt{R_2}}=\frac{OB}{OA}=\frac{I\sqrt{R_2}}{I\sqrt{R_1}},$

azaz

$\displaystyle I_1R_1=I_2R_2,$

tehát az ellenállásokra eső feszültségek megegyeznek.

Statisztika:

34 dolgozat érkezett.
4 pontot kapott:	Antalóczy Szabolcs, Beke Bálint, Csonka Illés, Gábriel Tamás, Hauber Henrik, Kovács Kinga, Kulcsár László, Kürti Gergely, Molnár Kristóf, Nemeskéri Dániel, Papp Marcell Imre, Schmercz Blanka, Somlán Gellért, Toronyi András, Varga 451 Erik, Vig Zsófia.
3 pontot kapott:	Albert Máté, Dóra Márton, Juhász Júlia.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	6 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2022. áprilisi fizika feladatai