 |
A P. 5438. feladat (2022. november) |
P. 5438. Egy spanyol gazdaságban a képen látható olajbogyópréssel törik péppé a bogyókat. A 90 cm átmérőjű zúzókerék tisztán gördülő síkja, amit az ábrán szaggatott vonal jelez, a tengelytől 75 cm távolságban van. A csacsi farka a tengelytől 180 cm távolságban verdesi a rudat, miközben az állat 2,4 m/s sebességgel körbe-körbe fut. A zúzókerékre egy 1 g tömegű olajbogyó ragad.
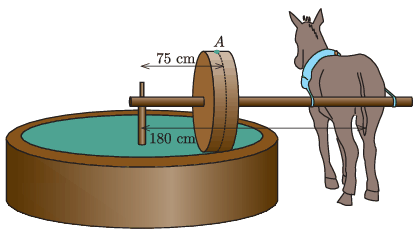
\(\displaystyle a)\) Mekkora az olajbogyó sebessége, amikor a felső \(\displaystyle A\) pontba ér?
\(\displaystyle b)\) Mekkora a olajbogyó gyorsulása az \(\displaystyle A\) pontban?
\(\displaystyle c)\) Mekkora és milyen irányú eredő erőt fejt ki a zúzókerék az olajbogyóra a legfelső \(\displaystyle A\) pontban?
Közli: Baranyai Klára, Veresegyház
(5 pont)
A beküldési határidő 2022. december 15-én LEJÁRT.
I. megoldás. \(\displaystyle a)\) A kerék tengelyeként szolgáló rúd egyenletesen forog körbe, pontjainak kerületi sebessége a tengelytől mért távolságukkal arányos. Ezért a megadott adatok alapján a kerék középpontja
\(\displaystyle v_{\rm{kp}}=\frac{75\,\rm{cm}}{180\,\rm{cm}}\cdot2{,}4\,\frac{\rm{m}}{\rm{s}}=1\,\frac{\rm{m}}{\rm{s}}\)
sebességgel halad. Mivel a kerék tisztán gördül, a legfelső \(\displaystyle A\) pont a középpont sebességének kétszeresével mozog, tehát az olajbogyó sebessége:
\(\displaystyle v_A = 2\,\frac{\rm m}{\rm s}. \)
Másképp is megkaphatjuk ezt az eredményt. A vízszintes rúd
\(\displaystyle \Omega=\dfrac{2{,}4~\rm m/s}{1{,}8~\rm m}=\frac 43~\frac1{\rm ~s}\)
szögsebességgel forog körbe, így a függőleges tengelytől \(\displaystyle R=0{,}75~\rm m\) távolságra lévő zúzókerék középpontja
\(\displaystyle v_\text{kp}=R\Omega=1~\dfrac{\rm m}{\rm s}\)
sebességgel halad. Az \(\displaystyle r=0{,}45~\rm m\) sugarú zúzókerék \(\displaystyle \omega\) szögsebességgel forog a vízszintes rúd körül, tehát az olajbogyó sebessége a kerék középpontjához képest \(\displaystyle r\omega\). A zúzókerék legalsó pontjának sebessége nulla, emiatt
\(\displaystyle R\Omega-r\omega=0, \qquad \text{azaz}\qquad r\omega=R\Omega= v_\text{kp}= 1\,\frac{\rm m}{\rm s}.\)
Az \(\displaystyle A\) pontban tehát az olajbogyó sebessége
\(\displaystyle v_A =R\Omega+r\omega= 2R\Omega=2\,\frac{\rm m}{\rm s}. \)
\(\displaystyle b)\) Az olajbogyó gyorsulásának kiszámítása nehezebb feladat. A bogyó mozgása – mint már leírtuk – két egyenletes körmozgásból tehető össze. A zúzókerék középpontja a függőleges tengely körül \(\displaystyle \Omega\) szögsebességgel forog, a gyorsulása (\(\displaystyle \boldsymbol a_\text{rúd}\)) tehát \(\displaystyle R\Omega^2\), iránya vízszintes és a tengely felé mutat. Az olajbogyó a zúzókerék középpontja körül \(\displaystyle \omega\) szögsebességű, \(\displaystyle r\) sugarú körpályán mozog, ehhez a mozgáshoz függőlegesen lefelé irányuló, \(\displaystyle r\omega^2\) nagyságú (\(\displaystyle \boldsymbol a_\text{kerék}\)) gyorsulás tartozik. Az olajbogyó teljes \(\displaystyle \boldsymbol a\) gyorsulása a talajhoz rögzített inerciarendszerben nem egyszerűen \(\displaystyle \boldsymbol a_\text{rúd}+\boldsymbol a_\text{kerék}\), hanem ehhez még egy harmadik tag, az ún. Coriolis-gyorsulás is hozzáadódik (lásd pl. a Négyjegyű függvénytáblázatok Tehetetlenségi erők alpontját). Azy \(\displaystyle \boldsymbol\Omega\) szögsebességgel forgó rendszerben a rendszerhez képest \(\displaystyle \boldsymbol v\) sebességgel mozgó test Coriolis-gyorsulása
\(\displaystyle \boldsymbol a_\text{Coriolis}=2 \boldsymbol\Omega \times\boldsymbol v.\)
Esetünkben \(\displaystyle \boldsymbol\Omega\) függőlegesen felfelé mutató \(\displaystyle \Omega\) nagyságú vektor, \(\displaystyle \boldsymbol v\) a kerék középpontjának pillanatnyi sebességével párhuzamos, vízszintes vektor. Ezek szerint a Coriolis-gyorsulás nagysága
\(\displaystyle a_\text{Coriolis}=2r\omega\Omega=2R\Omega^2,\)
iránya a rúddal párhuzamos és a függőleges tengely felé mutat.
Megjegyzés. 1. A Coriolis-gyorsulás szerepét jól illusztrálja a következő példa. Ha egy \(\displaystyle \Omega\) szögsebességgel forgó korongon a forgástengelytől \(\displaystyle R\) távolságban, a koronghoz képest \(\displaystyle v\) sebességgel körpályán mozog egy test, akkor a sebessége az inerciarendszerben \(\displaystyle R\Omega+v\), a gyorsulása pedig
\(\displaystyle a=\frac{v_\text{teljes}^2}{R}=\frac{(R\Omega+v)^2}{R}=R\Omega^2+\frac{v^2}{R}+2v\Omega.\)
A jobb oldal első tagja a korong pontjainak centripetális gyorsulása, a második tag a koronghoz viszonyított mozgás centripetális gyorsulása, a harmadik pedig a Coriolis-gyorsulás.
Az olajbogyó teljes gyorsulása végül:
\(\displaystyle \boldsymbol a_\text{teljes}=\boldsymbol a_\text{rúd}+\boldsymbol a_\text{kerék} +\boldsymbol a_\text{Coriolis},\)
amelynek vízszintes (,,befelé'' mutató) komponense
\(\displaystyle a_\text{be}=R\Omega^2+2R\Omega^2=3R\Omega^2=4{,}0~\frac{\rm m}{\rm s^2},\)
függőleges (lefelé mutató) összetevője
\(\displaystyle a_\text{le}=r\omega^2=2{,}22~\frac{\rm m}{\rm s^2},\)
a gyorsulásvektor nagysága pedig
\(\displaystyle a_\text{teljes}=\sqrt{a^2_\text{be}+a^2_\text{le}}= 4{,}58~\frac{\rm m}{\rm s^2}.\)
\(\displaystyle c)\) Az olajbogyóra két erő hat: az \(\displaystyle mg\) nagyságú nehézségi erő és a kerék felülete által kifejtett \(\displaystyle \boldsymbol F\) erő, melynek vízszintes komponense \(\displaystyle F_\text{be}\), függőleges komponense \(\displaystyle F_\text{fel}\). A mozgásegyenletek:
\(\displaystyle mg-F_\text{fel}=ma_\text{le}, \qquad \rightarrow \qquad F_\text{fel}=m(g-a_\text{le})=7{,}59\cdot 10^{-3}~\rm N,\)
illetve
\(\displaystyle F_\text{be}=ma_\text{be}=4{,}00\cdot 10^{-3}~\rm N.\)
Az erő nagysága
\(\displaystyle F=\sqrt{F^2_\text{fel}+F^2_\text{be}}=8{,}58\cdot 10^{-3}~\rm N,\)
a vízszintessel bezárt szöge
\(\displaystyle \alpha=\arctg\dfrac{F_\text{fel}}{F_\text{be}} =62{,}2^\circ. \)
II. megoldás. Az olajbogyó sebességét és gyorsulását a tehetetlenségi erők (a Coriolis erő és a centrifugális erő) elkerülésével is kiszámíthatjuk, ha mindvégig a talajhoz képest álló inerciarendszerben számolunk.
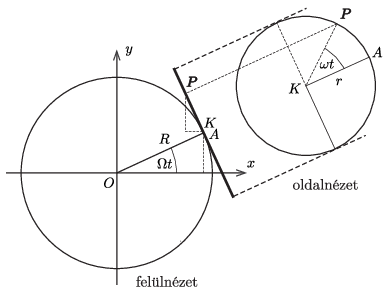
Az ábrán látható derékszögű koordináta-rendszerben a kerék \(\displaystyle K\) középpontjának koordinátái az olajbogyó \(\displaystyle A\) ponton való áthaladását követő \(\displaystyle t\) idő elteltével:
\(\displaystyle \boldsymbol r_K=(R\cos\Omega t, R\sin\Omega t, r).\)
Ennyi idő alatt a zúzókerék síkja \(\displaystyle \Omega t\) szöggel fordult el a függőleges tengely körül, a kerék rúd körüli elfordulása pedig \(\displaystyle \omega t\). Ez utóbbi miatt az olajbogyó \(\displaystyle P\) pontja \(\displaystyle r\sin \omega t\) távolságra kerül az \(\displaystyle A\) ponton átmenő függőleges egyenestől. Az ábráról leolvasható, hogy az olajbogyó koordinátái:
\(\displaystyle x(t)=R\cos\Omega t-r\sin\Omega t\cdot \sin \omega t,\)
\(\displaystyle y(t)=R\sin\Omega t+r\cos\Omega t\cdot \sin \omega t,\)
\(\displaystyle z(t)=r(1+\cos\omega t).\)
Az \(\displaystyle x(t)\) függvény a
\(\displaystyle \sin\alpha\sin\beta=\tfrac12\cos(\alpha-\beta)- \tfrac12\cos(\alpha+\beta)\)
azonosság felhasználásával így is felírható:
\(\displaystyle x(t)=R\cos\Omega t+\frac{r}2\cos(\Omega+\omega)t-\frac{r}2\cos(\Omega-\omega)t.\)
Ez három koszinuszos függvény összege, éppen olyanoké, mint amilyenek a kezdősebesség nélkül induló harmonikus rezgőmozgást írják le. Az analógia alapján a \(\displaystyle P\) pont \(\displaystyle x\) tengely irányú gyorsulása \(\displaystyle t=0\) pillanatban:
\(\displaystyle a_x(0)=-R\Omega^2-\frac{r}2 (\Omega+\omega)^2+\frac{r}2 (\Omega-\omega)^2= -R\Omega^2-2r\omega\Omega=-3R\Omega^2.\)
Hasonlóan olvashatjuk le, hogy
\(\displaystyle v_y(0)=2R\Omega,\qquad a_y(0)=0,\)
továbbá
\(\displaystyle v_z(0)=0,\qquad a_z(0)=-r\omega^2.\)
Megjegyzés. Hasonló módon számíthatjuk ki az olajbogyó gyorsulását abban a pillanatban, amikor az \(\displaystyle A\)-val átellenes helyzetben van (feltételezve, hogy még ott is hozzátapad a zúzókerékhez). Meglepő módon azt kapjuk, hogy a pálya legalsó pontjánál (vagyis ott, ahol az olajbogyó sebessége nulla) a vízszintes irányú gyorsulása \(\displaystyle +R\Omega^2\), tehát ,,kifelé'' gyorsulna. Ennek szemléletes magyarázata az, hogy az olajbogyó pályája nem egy \(\displaystyle R\) sugarú hengerpaláston történik, hanem egy \(\displaystyle R\) és egy \(\displaystyle \sqrt{R^2+r^2}\) sugarú henger között megy végbe. A bogyó bizonyos helyzetekben egyre jobban eltávolodik a függőleges tengelytől, emiatt lehet kifelé irányuló sebessége és gyorsulása is.
Statisztika:
65 dolgozat érkezett. 5 pontot kapott: Bencz Benedek. 4 pontot kapott: Bodré Zalán, Csiszár András, Elekes Dorottya, Halász Henrik, Kis Márton Tamás, Masa Barnabás, Szanyi Attila, Vincze Farkas Csongor. 3 pontot kapott: 20 versenyző. 2 pontot kapott: 14 versenyző. 1 pontot kapott: 10 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2022. novemberi fizika feladatai

