 |
A P. 5444. feladat (2022. november) |
P. 5444. Egy vékony, hosszú, függőleges, szigetelőrúdon súrlódásmentesen mozoghat egy kicsiny töltött golyócska. Ha egy ezzel azonos töltésű, ugyancsak kicsiny testet helyezünk a rúd tövébe, a mozgó golyó \(\displaystyle h_0\) magasságban lesz egyensúlyban. Milyen messzire távolíthatjuk el a rúdtól vízszintes irányba az alsó testet úgy, hogy a rúdon lévő golyó még egyensúlyban lehessen valahol? Milyen magasan van ez a hely?
Varga István (1952–2007) feladata nyomán
(6 pont)
A beküldési határidő 2022. december 15-én LEJÁRT.
Megoldás. Kiinduló helyzetben az elektromos taszítás tart egyensúlyt a rúdon lévő, \(\displaystyle Q\) töltésű test \(\displaystyle mg\) súlyával. Ennek megfelelően a testek feltételezett adataival kifejezve \(\displaystyle h_0=\sqrt{kQ^2/mg}\).
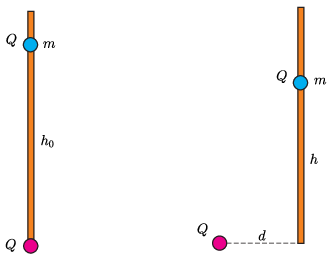
Egy általános helyzetben legyen \(\displaystyle d\) az alsó test távolsága a rúdtól, és jelölje \(\displaystyle h\) azt a magasságot, ahol a rúdon lévő test egyensúlyban van! Ekkor az eletromos erő függőleges komponense tart egyensúlyt a rúdon lévő test súlyával, tehát
\(\displaystyle \frac{kQ^2}{d^2+h^2}\frac{h}{\sqrt{d^2+h^2}}=mg.\)
Ebből a testek adatait kiküszöbölve a
\(\displaystyle \frac{h h_0^2}{\left(h^2+d^2\right)^{3/2}}=1\)
egyenletet kapjuk, amit a következő alakra rendezünk:
\(\displaystyle \left(h^2+d^2\right)^{3}-\left(h^2+d^2\right)h_0^4+d^2h_0^4=0. \)
A könnyebb írásmód kedvéért legyen \(\displaystyle x=\left(h^2+d^2\right)\), tehát az egyenletünk
\(\displaystyle x^3-xh_0^4+d^2h_0^4=0.\)
Ez egy harmadfokú egyenlet, egy vagy három valós gyökkel. Elemezzük a bal oldalon álló függvény alakját! \(\displaystyle d=0\) esetén minden szimmetrikus, a gyökök pedig \(\displaystyle \pm h_0^2\) és \(\displaystyle 0\). \(\displaystyle d\)-t növelve két pozitív és egy negatív gyök adódik, de ez utóbbi nem fizikai megoldás, hiszen \(\displaystyle x>0\).
Egy bizonyos \(\displaystyle d_{\rm max}\) mellett a két pozitív gyök egybeesik, ha pedig \(\displaystyle d>d_{\rm max}\), az egyenletnek nincs pozitív megoldása. A \(\displaystyle d=d_{\rm max}\) esethez tartozó pozitív gyök legyen \(\displaystyle x_0\)! Ez egy kettős gyök, és mivel az összes gyök összege nulla (hiszen nincs kvadratikus tag az egyenletben) a harmadik gyök \(\displaystyle -2x_0\). Ennek megfelelően az
\(\displaystyle x^3-xh_0^4+d_{\rm max}^2h_0^4=0\)
egyenlet azonos az
\(\displaystyle (x-x_0)^2(x+2x_0)=x^3-3x_0^2 x+2x_0^3=0\)
egyenlettel. Ebből
\(\displaystyle 3x_0^2=h_0^4,\qquad \ \mbox{és}\qquad \ 2x_0^3=d_{\rm max}^2h_0^4,\)
azaz
\(\displaystyle d_{\rm max}=\sqrt[4]{\frac{4}{27}}h_0.\)
Ilyenkor
\(\displaystyle h=\sqrt[4]{\frac{1}{27}}h_0.\)
Megjegyzés. Bár a feladat paraméteres, numerikusan is megoldható. A harmadfokú egyenlet \(\displaystyle h_0^6\)-nal való osztásával a
\(\displaystyle \xi^3-\xi+(d/h_0)^2=0\)
egyenletre jutunk (ahol \(\displaystyle \xi=x/h_0^2\)). Ennek az egyenletnek akkor van pont egy pozitív megoldása, ha az
\(\displaystyle f(\xi)=\xi^3-\xi+(d/h_0)^2\)
függvény éppen érinti az \(\displaystyle f=0\) tengelyt. Az a \(\displaystyle \xi_0\) érték, ahol ez lehetséges (ahol az \(\displaystyle f(\xi)\)-nek lokális minimuma van) akár deriválással (\(\displaystyle \xi_0=1/\sqrt3\)), akár numerikusan \(\displaystyle (\xi_0\approx 0{,}58)\) megtalálható, és ebből a \(\displaystyle d_{\rm max}/h_0\) megkapható:
\(\displaystyle d_{\rm max}/h_0 = \sqrt{\xi_0-\xi_0^3}=\sqrt[4]{\frac{4}{27}}\approx 0{,}62. \)
Statisztika:
27 dolgozat érkezett. 6 pontot kapott: Bencz Benedek, Bodré Zalán, Brezina Gergely, Chrobák Gergő, Csilling Dániel, Elekes Dorottya, Fehérvári Donát, Flóring Balázs, Halász Henrik, Hegedűs Máté Miklós, Lévai Dominik Márk, Molnár Kristóf, Molnár Zétény, Seprődi Barnabás Bendegúz, Tárnok Ede , Tatár Ágoston, Tóth Kolos Barnabás. 5 pontot kapott: Kovács Barnabás, Nemeskéri Dániel, Papp Marcell Imre. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2022. novemberi fizika feladatai
