 |
A P. 5483. feladat (2023. április) |
P. 5483. Egy elhanyagolható tömegű, \(\displaystyle R\) sugarú abroncs egyik átmérőjének két végpontjába egy \(\displaystyle m\), illetve egy \(\displaystyle M=2m\) tömegű, pontszerű nehezéket erősítettünk. A függőleges síkú abroncsot súrlódásmentes asztallapra helyezzük úgy, hogy kezdetben a két nehezék azonos függőleges egyenesen helyezkedik el (a nehezebb van felül). Az abroncsot ebből az instabil egyensúlyi állapotból elengedjük.
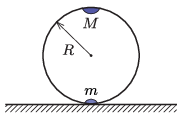
\(\displaystyle a)\) Mekkora az abroncs középpontjának sebessége, amikor az \(\displaystyle M\) tömegű nehezék eléri pályájának legalsó pontját?
\(\displaystyle b)\) Mekkora az \(\displaystyle a)\) esetben az asztalra ható nyomóerő?
Közli: Vigh Máté, Biatorbágy
(5 pont)
A beküldési határidő 2023. május 15-én LEJÁRT.
Megoldás. Legyen a testek sebessége a kérdéses pillanatban az ábrán jelölt irányításokkal \(\displaystyle v_1\) és \(\displaystyle v_2\).
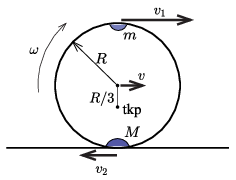
A rendszerre nem hat vízszintes irányú külső erő, emiatt a vízszintes irányú összimpulzus nulla marad:
| \(\displaystyle (1)\) | \(\displaystyle mv_1-2mv_2=0, \qquad \text{tehát}\qquad v_1=2v_2.\) |
Mivel az asztallap súrlódásmentes, a mechanikai energia megmaradásának törvénye is alkalmazható:
\(\displaystyle \frac{m}2v_1^2+\frac{M}2v_2^2=Mg\cdot 2R-mg\cdot 2R,\)
ahonnan \(\displaystyle M=2m\) és (1) felhasználásával kapjuk, hogy
\(\displaystyle v_1=\sqrt{\frac{8}{3}Rg} \qquad\text{és}\qquad v_2=\sqrt{\frac{2}{3}Rg}.\)
\(\displaystyle a)\) Az abroncs középpontjának sebessége
\(\displaystyle v=\frac{v_1-v_2}{2}=\sqrt{\frac{Rg}{6} }.\)
\(\displaystyle b)\) I. megoldás. Az abroncs szögsebessége a vizsgált helyzetben
\(\displaystyle \omega=\frac{v}{R/3}=\frac{v_1-v_2}{2R/3}=\sqrt{\frac{3g}{2R} }.\)
A rendszer tömegközéppontja \(\displaystyle s=R/3\) távol van az abroncs középpontjától, így az abroncshoz képest \(\displaystyle s\omega^2\) nagyságú, függőlegesen felfelé irányuló gyorsulással mozog. (Az abroncs középpontja vízszintes irányban ide-oda mozog, éppen úgy, hogy a tömegközéppont vízszintes irányba ne mozduljon el.)
Ha az asztalra ható nyomóerő \(\displaystyle N\), ennek függőlegesen felfelé mutató ellenereje is \(\displaystyle N\) nagyságú, így a függőleges irányú mozgás Newton-egyenlete:
\(\displaystyle N-3mg=3m \ s\omega^2=\frac32 mg,\)
vagyis \(\displaystyle N=\frac92mg.\)
II. megoldás. Az \(\displaystyle N\) nyomóerőt másképpen is megkaphatjuk. Ahogy már láttuk, a kérdéses pillanatban az abroncs középpontja (az ábrán is láthatóan jobbra) \(\displaystyle v\) sebességgel mozog:
\(\displaystyle v=\frac{v_1-v_2}{2}=\frac{v_2}{2}=\sqrt{\frac{Rg}{6} }.\)
Üljünk be az abroncs középpontjával együtt mozgó rendszerbe, ami ebben a pillanatban inerciarendszer, mert ekkor nincs vízszintes gyorsulása a karika középpontjának.
Ebben a rendszerben mindkét nehezék \(\displaystyle 3v\) sebességgel mozog, így mindkettőnek a gyorsulása
\(\displaystyle a_{\rm{cp}}=\frac{(3v)^2}{R}=\frac{3}{2}g.\)
A felső nehezéket az abroncs \(\displaystyle N_1=ma_{\rm{cp}}-mg\) erővel nyomja lefelé, az alsót pedig \(\displaystyle N_2=2ma_{\rm{cp}}+2mg\) erővel nyomja felfelé. Ezek előjeles összege adja meg az asztalra ható nyomóerőt:
\(\displaystyle N=N_2-N_1=(2ma_{\rm{cp}}+2mg)-(ma_{\rm{cp}}-mg)=ma_{\rm{cp}}+3mg=m\frac{3}{2}g+3mg=\frac92mg.\)
A rendszer tömegközéppontjának eredő (felfelé mutató) gyorsulását úgy kaphatjuk meg, ha az eredő erőt elosztjuk a teljes tömeggel:
\(\displaystyle a=\frac{N-3mg}{3m}=\frac{g}{2},\)
ami megegyezik az előzőekben tárgyalt
\(\displaystyle s\omega^2=\frac{R}{3}\frac{3g}{2R}=\frac{g}{2}\)
gyorsulással.
Felmerülhet az a kérdés is, hogyan lehet az abroncs nyomóerejét úgy kiszámítani a két nehezék gyorsulásából, hogy nem ülünk be a \(\displaystyle v\) sebességgel mozgó rendszerbe. Megmutatható, hogy mozgása során mindkét nehezék ellipszispályán mozog, de ezek különböző ellipszisek. A nagyobb nehezék ,,álló'' ellipszisen mozog, melynek fél-nagytengelye \(\displaystyle R\), fél-kistengelye pedig \(\displaystyle 2R/3\). A kisebb tömegű nehezék ,,fekvő" ellipszisen mozog, melynek fél-kistengelye \(\displaystyle R\), míg fél-nagytengelye \(\displaystyle 4R/3\). Az ellipszis nagytengelyének végpontjaiban a görbületi sugár \(\displaystyle r_{\rm{g1}}=b^2/a\), ahol \(\displaystyle a\) a fél-nagytengely és \(\displaystyle b\) a fél-kistengely, míg a kistengely végpontjaiban \(\displaystyle r_{\rm{g2}}=a^2/b\) a görbületi sugár. Így a nagyobb nehezék mozgására nézve a görbületi sugár a legalsó pontban
\(\displaystyle r_{\rm{g1}}=\frac{(2R/3)^2}{R}=\frac{4}{9}R,\)
míg a kisebb nehezék pályájának görbületi sugara a legfelső pontban
\(\displaystyle r_{\rm{g2}}=\frac{(4R/3)^2}{R}=\frac{16}{9}R.\)
A gyorsulást úgy számíthatjuk ki, hogy a sebesség négyzetét elosztjuk a görbületi sugárral. A nagyobb nehezék \(\displaystyle 2v\) sebességgel mozog, míg a kisebbik \(\displaystyle 4v\) sebességgel. A nagyobb gyorsulása
\(\displaystyle a_{\rm{cp}}=\frac{(2v)^2}{r_{\rm{g1}}}=\frac{(2v)^2}{(4R/9)}=\frac{9v^2}{R}=\frac{3}{2}g.\)
A kisebbik nehezék kétszer gyorsabb, \(\displaystyle 4v\) sebességgel mozog, tehát a gyorsulása
\(\displaystyle a_{\rm{cp}}=\frac{(4v)^2}{r_{\rm{g2}}}=\frac{(4v)^2}{(16R/9)}=\frac{9v^2}{R}=\frac{3}{2}g.\)
Láthatjuk, hogy a két gyorsulás megegyezik, visszakaptuk a mozgó rendszer használatával kiszámított értékeket. Egymáshoz képest mozgó inerciarendszerekben a gyorsulásoknak meg kell egyezniük. Abban a rendszerben, ahol a kör középpontja áll, és mindkét test ugyanazon a körpályán, ugyanakkora kerületi sebességgel mozog, a gyorsulások nagysága megegyezik, tehát az asztallaphoz rögzített rendszerben is ugyanazokat a gyorsulásokat kell kapnunk. Nehézséget jelent, hogy ilyenkor a pálya görbületi sugarát kell használnunk a centripetális gyorsulás meghatározásakor.
Statisztika:
33 dolgozat érkezett. 5 pontot kapott: Bencz Benedek, Csilling Dániel, Kis Márton Tamás, Seprődi Barnabás Bendegúz. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2023. áprilisi fizika feladatai
