A P. 5485. feladat (2023. április)

P. 5485. Egy szabályos ötszög csúcsait az oldalak mentén az ábrán látható módon egyforma ellenálláshuzalokkal összekötjük. Egy másik szabályos ötszögbe az átlók mentén helyezünk el ellenálláshuzalokat, így azok egy ötágú csillagot képeznek. (Az ellenálláshuzalok szigeteltek és csak az ötszög csúcsaiban érintkeznek.)

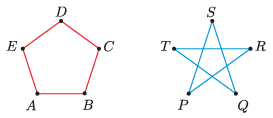
Az ötszögek szomszédos csúcsai között mérhető eredő ellenállás (\(\displaystyle R_{AB}\), illetve \(\displaystyle R_{PQ}\)) a két kapcsolásban ugyanakkora. Melyik kapcsolásban és hányszor nagyobb az átlók végpontjai között mérhető eredő (\(\displaystyle R_{AC}\), illetve \(\displaystyle R_{PR}\)) ellenállás?

Közli: Bertalan Zoltán, Békéscsaba

(4 pont)

A beküldési határidő 2023. május 15-én LEJÁRT.

Megoldás. Az első esetben az ötszög oldalaira helyezett ellenállásokat jelöljük \(\displaystyle R_\textrm{o}\)-val, a másodikban az átlókat alkotó huzalok ellenállása legyen \(\displaystyle R_\textrm{á}\)! Ezekkel

\(\displaystyle R_{AB}=\left(\frac{1}{R_\textrm{o}}+\frac{1}{4R_\textrm{o}}\right)^{-1}=\frac{4}{5}R_\textrm{o}, \)

illetve

\(\displaystyle R_{PQ}=\left(\frac{1}{2R_\textrm{á}}+\frac{1}{3R_\textrm{á}}\right)^{-1}=\frac{6}{5}R_\textrm{á}. \)

Ha ez a két érték egyenlő, akkor

\(\displaystyle R_\textrm{o}=\frac{3}{2}R_\textrm{á}. \)

Ugyanakkor

\(\displaystyle R_{AC}=\left(\frac{1}{2R_\textrm{o}}+\frac{1}{3R_\textrm{o}}\right)^{-1}=\frac{6}{5}R_\textrm{o}, \)

és

\(\displaystyle R_{PR}=\left(\frac{1}{R_\textrm{á}}+\frac{1}{4R_\textrm{á}}\right)^{-1}=\frac{4}{5}R_\textrm{á}. \)

Innen

\(\displaystyle R_{AC}=\frac{9}{4}R_{PR}. \)

Megjegyzés. A \(\displaystyle PQRST\) csillag nem csupán egy ötszög átlói által alkotott idom, hanem maga is egy ügyesen ,,összehajtogatott" ötszög. Ennek a csúcsai sorban \(\displaystyle PRTQS\). Ez magyarázza, hogy az első-szomszéd és másod-szomszéd csúcsok között mérhető ellenállások aránya a két alakzatnál pont egymás reciproka.

Statisztika:

42 dolgozat érkezett.
4 pontot kapott:	Bocor Gergely, Bodré Zalán, Boér Panna Rita, Bottyán Márton Péter, Chrobák Gergő, Csilling Dániel, Dercsényi Bence, Éger Viktória, Fehérvári Donát, Fórizs Borbála, Gerendás Roland, Halász Henrik, Hegedűs Máté Miklós, Kátai Ferdinánd, Kis Márton Tamás, Klement Tamás, Kovács Barnabás, Lengyel Szabolcs, Molnár Kristóf, Nemeskéri Dániel, Schmercz Blanka, Seprődi Barnabás Bendegúz, Szécsényi-Nagy Rudolf, Tomesz László Gergő, Vásárhelyi István Péter.
3 pontot kapott:	Beke Bálint, Bogdán Benedek, Csiszár András, Fajszi Karsa, Molnár Zétény, Papp Marcell Imre, Waldhauser Miklós.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2023. áprilisi fizika feladatai