A P. 5487. feladat (2023. április)

P. 5487. Egy $\displaystyle n$ törésmutatójú félhenger síklapját befoncsorozzuk. Az ábrának megfelelően a félhengert egy lézersugárral vízszintesen megvilágítjuk. Mekkora $\displaystyle \alpha$ értéknél lesz a kilépő fénysugár éppen függőleges? Mennyi legyen $\displaystyle n$ minimális értéke, hogy ilyen sugármenet lehetséges legyen?

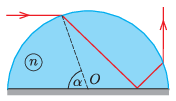
Közli: Cserti József, Budapest

(5 pont)

A beküldési határidő 2023. május 15-én LEJÁRT.

Megoldás. Tükrözzük a félgömböt és a fénysugár útvonalát a foncsorozott felületre. Így egy teljes hengeren áthaladó, kétszer megtörő fénysugarat kapunk, amely a beesés irányához képest összesen $\displaystyle 90^\circ$-os szögben térül el.

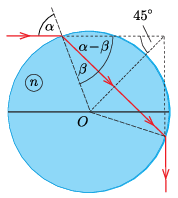
Az ábráról leolvashatjuk, hogy a beesési szög és a törési szög különbsége $\displaystyle 45^\circ$, vagyis

$\displaystyle \beta=\alpha-45^\circ.$

Másrészt a törési törvény szerint

$\displaystyle \sin \beta =\frac{\sin \alpha}{n},$

vagyis

$\displaystyle \sin(\alpha-45^\circ)\equiv \frac1{\sqrt2}(\sin\alpha-\cos\alpha)=\frac{\sin \alpha}{n},$

amiből

$\displaystyle n=\frac{\sqrt2}{1-\ctg\alpha}$

következik. Mivel $\displaystyle \alpha$ hegyesszög (vagy legfeljebb derékszög), $\displaystyle \ctg\alpha\ge 0$, és így $\displaystyle n\ge\sqrt2$.

Statisztika:

11 dolgozat érkezett.
5 pontot kapott:	Bencz Benedek, Fehérvári Donát, Halász Henrik, Schmercz Blanka, Seprődi Barnabás Bendegúz, Szabó Zsombor, Waldhauser Miklós.
4 pontot kapott:	Chrobák Gergő, Richlik Márton.
0 pontot kapott:	1 versenyző.

A KöMaL 2023. áprilisi fizika feladatai