 |
A P. 5489. feladat (2023. április) |
P. 5489. Egy olyan téglalap alakú keretet készítettünk, amelynek \(\displaystyle a\) hosszúságú vízszintes oldalai merev, egyenes, \(\displaystyle m\) tömegű drótszálak, \(\displaystyle b\) hosszúságú függőleges oldalai pedig vékony, elhanyagolható tömegű cérnaszálak.
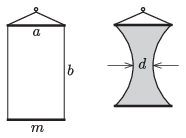
A keretet az egyik drótszálnál fogva mosogatószeres oldatba mártottuk, majd kiemeltük. A kialakuló hártya mérete a közepénél \(\displaystyle d\) értékre csökkent. Mekkora a folyadék felületi feszültsége?
Adatok: \(\displaystyle a=5\) cm, \(\displaystyle b=8\) cm, \(\displaystyle d=3{,}6\) cm, \(\displaystyle m=2{,}6\) g.
Varga István (1952–2007) feladata
(6 pont)
A beküldési határidő 2023. május 15-én LEJÁRT.
I. megoldás. A cérnaszálak által kifejtett \(\displaystyle F\) erő és a cérnaszál görbületi sugara között fennálló összefüggés
| \(\displaystyle (1)\) | \(\displaystyle F=2\sigma R,\) |
ahol \(\displaystyle 2\sigma\) a hártya két oldalának együttes felületi feszültsége. (Ezt pl. a cérnaszál kicsiny darabkájára ható erők egyensúlyából kaphatjuk meg.) Mivel \(\displaystyle F\) a cérnaszál mentén nem változik, \(\displaystyle R\) is állandó, tehát a cérnaszál körív alakot vesz fel.
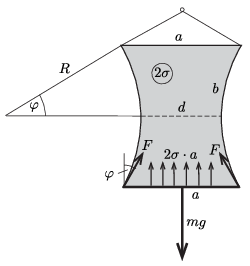
Az ábra jelöléseit követve a
| \(\displaystyle (2)\) | \(\displaystyle b=2\varphi R,\) |
és az
| \(\displaystyle (3)\) | \(\displaystyle R(1-\cos\varphi)=\frac{a-d}{2}\) |
geometriai feltételeket, valamint az alsó drótszál erőegyensúlyának
| \(\displaystyle (4)\) | \(\displaystyle mg=2\sigma a+2F\cos\varphi\) |
feltételét írhatjuk fel.
A (2) és (3) egyenleteket összeszorozva kapjuk, hogy
\(\displaystyle \frac{1-\cos\varphi}{\varphi}=\frac{a-d}{b}=0{,}175,\)
amit
| \(\displaystyle (5)\) | \(\displaystyle 2\sin^2\frac{\varphi}2=0{,}175\,\varphi \) |
alakban is felírhatunk. Ennek a trigonometrikus egyenletnek (mint azt számítógépes segítséggel könnyen meghatározhatjuk) \(\displaystyle \varphi\approx0{,}354\) rad a megoldása. Ezt elemi úton is megkaphatjuk, ha a viszonylag kis szögekre érvényes
\(\displaystyle \sin\frac{\varphi}2\approx \frac{\varphi}2\)
összefüggést alkalmazzuk. Ennek megfelelően (5) közelítő, nullától különböző megoldása:
\(\displaystyle \varphi\approx 2\cdot 0{,}175=0{,}350,\)
ami csak 1%-kal tér el a pontosabb eredménytől.
(1) és (2) szerint
\(\displaystyle F=\frac{b\sigma}\varphi,\)
amit (4)-be helyettesítve kapjuk, hogy
| \(\displaystyle (5)\) | \(\displaystyle 2\sigma\left(a+b\,\frac{\cos\varphi}{\varphi}\right)=mg,\) |
ahonnan az adatok és a kiszámított \(\displaystyle \varphi\) szög behelyettesítése után a
\(\displaystyle \sigma\approx 0{,}05\ \frac{\rm N}{\rm m}\)
eredmény adódik. Ez kicsit kisebb, mint a víz felületi feszültsége, amit a mosogatószer okozhatott.
II. megoldás. Az egyensúlyi helyzetet (és abból a felületi feszültséget) a rendszer energiájának vizsgálatával is meghatározhatjuk. Az elrendezés összes energiája az alsó drótszál \(\displaystyle E_1\) helyzeti energiájából és a hártya felületével arányos \(\displaystyle E_2\) energiából tevődik össze.
Válasszuk független változónak az I. megoldás ábráján látható \(\displaystyle \varphi\) szöget, és a cérnaszálak görbületi sugarát (2) szerint fejezzük ki \(\displaystyle \varphi\)-vel: \(\displaystyle R=b/(2\varphi)\). A nehezék helyzeti energiája (annak nullpontját a felső drótszál magasságánál rögzítve)
\(\displaystyle E_1(\varphi)=-mg\cdot 2R\sin\varphi=-mgb\frac{\sin\varphi}{\varphi}.\)
A hártya felületének \(\displaystyle T\) nagysága egy téglalap, két körcikk és négy derékszögű háromszög területének előjeles összegeként kapható meg. Ennek megfelelően a felületi energia:
\(\displaystyle E_2(\varphi)=2\sigma T(\varphi)=2\sigma \,ab\frac{\sin\varphi}{\varphi}+\frac{\sigma\, b^2}{\varphi^2}(\sin\varphi\cos\varphi-\varphi),\)
a rendszer teljes energiája pedig
\(\displaystyle E(\varphi)=(2\sigma \,ab-mgb)\frac{\sin\varphi}{\varphi}+\frac{\sigma\, b^2}{\varphi^2}(\sin\varphi\cos\varphi-\varphi).\)
Az egyensúlyi helyzetben a teljes energia minimális, vagyis az \(\displaystyle E(\varphi)\) függvény deriváltja nulla. Ez a feltétel éppen az (5) egyenletre vezet, amiből (\(\displaystyle d\) segítségével kiszámítva \(\displaystyle \varphi\)-t) a felületi
feszültség is kiszámítható.
Megjegyzések. 1. A II. megoldásnak az az előnye az I. megoldáshoz képest, hogy nem kell figyelembe vennie a cérnaszálakat feszítő erőket. Hátránya, hogy az eredményhez csak a differenciálszámítás képletei segítségével, vagy az \(\displaystyle E(\varphi)\) függvény grafikonjának vizsgálatával juthatunk el.
2. Csábító, de hibás az a gondolat, hogy az egyensúlyi helyzetet az alsó drót helyzeti energiájának növekedésének és a felületi energia csökkenésének egyenlőségéből számítsuk ki. A kiindulási helyzetnek a folyadékból éppen kiemelt keretet választva a gravitációs helyzeti energia növekedése nem egyezik meg a felületi energia csökkenésével, hiszen a kettő előjeles összege nem nulla. A folyadékból kiemelt drótkeret alsó szálát a folyadékhártya felrántja, az csillapodó rezgőmozgásba kezd, majd az egyensúly beálltáig az összenergia egy része hőt fejlesztve disszipálódik. Az energiaváltozások egyenlősége csak az egyensúlyi helyzetből gondolatban kicsit kimozdított rendszerre igaz. Az ilyen ,,elképzelt'' (virtuális) elmozdulásokra alapozott megfontolást virtuálius munka elvének nevezik.
Statisztika:
5 dolgozat érkezett. 6 pontot kapott: Bencz Benedek. 3 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2023. áprilisi fizika feladatai
