 |
A P. 5516. feladat (2023. október) |
P. 5516. Egy vízszintes tengely körül megpörgetett pingponglabda függőlegesen az asztallapra esik. A vékony gömbhéjnak tekinthető labda tömege \(\displaystyle m\), sugara \(\displaystyle R\), sebessége a leérkezéskor \(\displaystyle v_0\), szögsebessége \(\displaystyle \omega_0=v_0/R\), tehetetlenségi nyomatéka \(\displaystyle \Theta=\frac23 mR^2\). A csúszási és a tapadási súrlódási együttható egyaránt \(\displaystyle \mu\). Tekintsük az ütközést pillanatszerűnek és tökéletesen rugalmasnak (azaz legyen a labda tömegközépponti sebességének asztalra merőleges vetülete ütközés előtt és után azonos nagyságú).
Mekkora és milyen irányú lesz a labda sebessége az ütközés után? Mekkora lesz a szögsebessége?
Közli: Balogh Péter, Gödöllő
(A nyomtatott szövegben az egyik képlet hibásan jelent meg, helyesen \(\displaystyle \omega_0=v_0/R\).)
(6 pont)
A beküldési határidő 2023. november 15-én LEJÁRT.
Megoldás. Az 1. ábra az ütközés előtti \(\displaystyle (a)\) pillanatot, az ütközéskor fellépő erőket \(\displaystyle (b)\), és végül az ütközést követő pillanatot \(\displaystyle (c)\) mutatja.
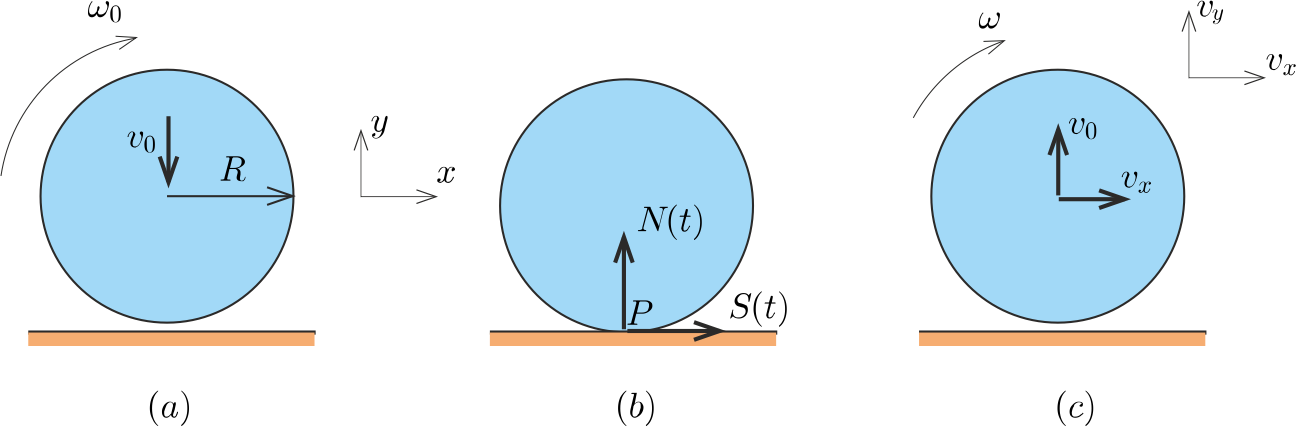
1. ábra
Az ütközés ,,pillanatszerű'' (valójában nagyon rövid idő alatt végbemenő) folyamat. A súrlódási erő időben gyorsan változó, de csak nagyon rövid (\(\displaystyle \Delta t\)) ideig fellépő \(\displaystyle S(t)\) függvénnyel adható meg. (\(\displaystyle S(t)\) konkrét alakjára nem lesz szükségünk.) Ezt az erőlökést
\(\displaystyle I_S\equiv \overline{S(t)}\cdot \Delta t\)
módon lehetne kiszámítani (a felülvonás az időbeli átlagértéket jelöli). Newton törvénye szerint az erőlökés a lendületváltozással egyezik meg:
| \(\displaystyle (1)\) | \(\displaystyle I_S=mv_x,\) |
ahol \(\displaystyle v_x\) a pingponglabda sebességének vízszintes komponense az ütközés után.
Az ütközés során az asztallap valamekkora \(\displaystyle N(t)\) nagyságú, függőlegesen felfelé irányuló erővel nyomja a labdát, és ez
\(\displaystyle I_N\equiv \overline{N(t)}\cdot \Delta t\)
erőlökést eredményez. (Mivel az ütközés ,,pillanatszerű'', \(\displaystyle \overline{N(t)}\gg mg\), a labdára ható nehézségi erőt tehát az ütközés alatt elhanyagolhatjuk.) A labda függőleges (\(\displaystyle y\) irányú) sebessége az ütközés során \(\displaystyle v_y=-v_0\)-ról \(\displaystyle +v_0\)-ra változik, tehát
| \(\displaystyle (2)\) | \(\displaystyle I_N=2mv_0.\) |
A súrlódási erő hatására a labda szögsebessége a kezdeti \(\displaystyle \omega_0\)-ról valamekkora \(\displaystyle \omega\)-ra csökken. A labdára ható erők hatásvonalai az ütközés \(\displaystyle P\) pontjára illeszkednek, így erre a pontra nézve nincs forgatónyomatékuk. A forgómozgás törvényei szerint tehát a labda \(\displaystyle P\) pontra vonatkoztatott perdülete (ami egyrészt a labda forgásából, másrészt a tömegközépponjának mozgásából származik) az ütközés során változatlan marad:
| \(\displaystyle (3)\) | \(\displaystyle \Theta \omega_0=\Theta \omega+mv_xR.\) |
Megjegyzés. Ezt az eredményt úgy is megkaphatjuk, hogy az (1)-ből kiszámított \(\displaystyle I_S\) erőlökésnek a pingponglabda tömegközéppontjára vonatkoztatott forgatónyomatékát a perdületváltozással tesszük egyenlővé:
\(\displaystyle I_SR=mv_xR=-\Theta(\omega-\omega_0).\)
Tudjuk még, hogy mindaddig, amíg a labda csúszik az asztalon, minden pillanatban fennáll: \(\displaystyle S(t)=\mu N(t)\), és így
\(\displaystyle \overline{S(t)}=\mu \overline{N(t)}.\)
A továbbiakban két esetet különböztethetünk meg.
I. eset. A súrlódási együttható nem túl nagy, vagyis nem halad meg egy bizonyos (később kiszámítandó) ,,kritikus értéket'' (\(\displaystyle \mu<\mu_\text{krit.}\)), és emiatt a labda az ütközés során mindvégig csúszik az asztalon. Ilyenkor az erőlökések is ugyanolyan arányban állnak egymással, mint a pillanatnyi erőnagyságok, vagyis
| \(\displaystyle (4)\) | \(\displaystyle I_S=\mu I_N.\) |
Az (1), (2) és (4) egyenletek szerint a labda középpontjának sebessége az ütközés után:
\(\displaystyle v_x=2\mu\,v_0,\)
a szögsebessége pedig (3) szerint
\(\displaystyle \omega=(1-3\mu)\frac{v_0}{R}.\)
A folyamatos csúszás feltétele: \(\displaystyle R\omega>v_x\), ami
\(\displaystyle \mu<\frac15=\mu_\text{krit.} \)
esetén teljesül.
II. eset. Ha \(\displaystyle \mu>\frac15\), akkor még az ütközés vége előtt \(\displaystyle v_x\) és \(\displaystyle R\omega\) egyenlő nagyságúvá válik, vagyis a labda a továbbiakban már nem csúszik, hanem tisztán gördül az asztalon. Ilyenkor (3) szerint
| \(\displaystyle (5)\) | \(\displaystyle v_x=R\omega=\frac25\,v_0.\) |
Ez a sebesség a továbbiakban nem változik, mert a (tapadási) súrlódási erő hirtelen nullára csökken.
Megjegyzés. Jóllehet a feladat szövege nem kéri az ütközés folyamatának részletes leírását, tanulságos lehet ennek tárgyalása is. A folyamat időbeli lefolyását az asztal és a labda rugalmas tulajdonságaitól függő \(\displaystyle N(t)\) erő ismerete nélkül nem tudjuk megadni, de a függőleges irányú \(\displaystyle v_y\) sebesség függvényében ki tudjuk számítani a tömegközéppont vízszintes sebességét és a labda kerületi sebességét is. (Ha \(\displaystyle N(t)=\) állandó teljesülne, akkor \(\displaystyle v_y\) az időnek lineáris függvénye lenne, tehát ez a két változó egy állandó szorzófaktor erejéig megegyezne. A valós helyzet ettől nyilván különböző.)
Jelöljük az ütközés kezdete után \(\displaystyle t\) idővel későbbi pillanatban a labda középpontjának sebességkomponenseit \(\displaystyle v_x(t)\)-vel és \(\displaystyle v_y(t)\)-vel, a szögsebességet \(\displaystyle \omega(t)\)-vel, az asztal által \(\displaystyle t\) idő alatt kifejtett erőlökés komponenseit pedig \(\displaystyle I_N(t)\)-vel és \(\displaystyle I_S(t)\)-vel.
A lendületváltozásokra és a perdületmegmaradásra a következő egyenleteket írhatjuk fel:
| \(\displaystyle (1')\) | \(\displaystyle I_S(t)=mv_x(t), \) |
| \(\displaystyle (2')\) | \(\displaystyle I_N(t)=mv_y(t)+mv_0,\) |
| \(\displaystyle (3')\) | \(\displaystyle \frac23mR^2\omega_0=mRv_x(t)+\frac23mR^2\omega(t),\) |
és végül a csúszási szakaszra érvényes
| \(\displaystyle (4')\) | \(\displaystyle I_S(t)=\mu I_N(t), \qquad\text{ameddig}\qquad v_x(t)<R\omega(t).\) |
A fenti egyenletrendszer megoldása \(\displaystyle \mu<\mu_\text{krit.}=\frac15\) esetén:
\(\displaystyle v_x(t)=\mu v_y(t)+\mu v_0,\)
\(\displaystyle R\omega(t)=v_0\left(1-\frac{3\mu}{2}\right)-\frac{3\mu}{2}v_y(t).\)
Ezek a sebességfüggvények pl. \(\displaystyle \mu=0{,}15\)-re a 2. ábrán látható grafikonnal szemléltethetők.
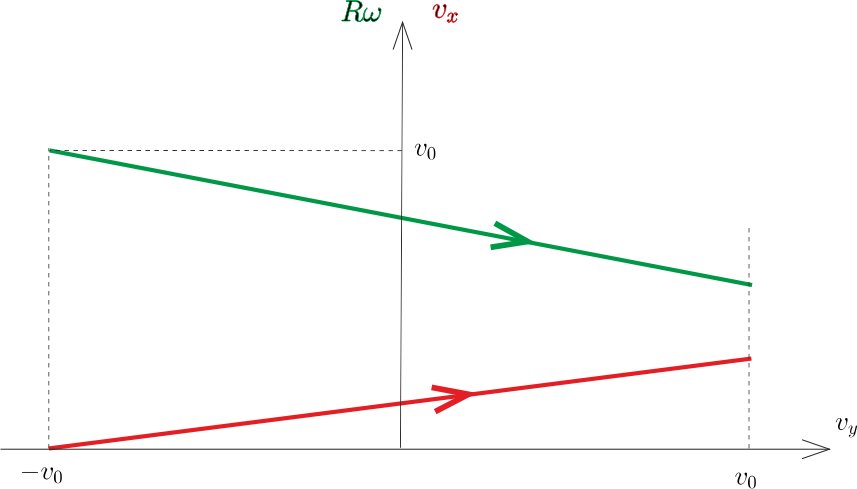
2. ábra
Amennyiben \(\displaystyle \mu=0{,}4>\mu_\text{krit.}\), a labda tömegközéppontjának vízszintes sebessége és a kerületi sebessége már az ütközés befejeződése előtt egyenlővé válik, és ettől a pillanattól kezdve tiszta gördülés esete valósul meg (3. ábra).
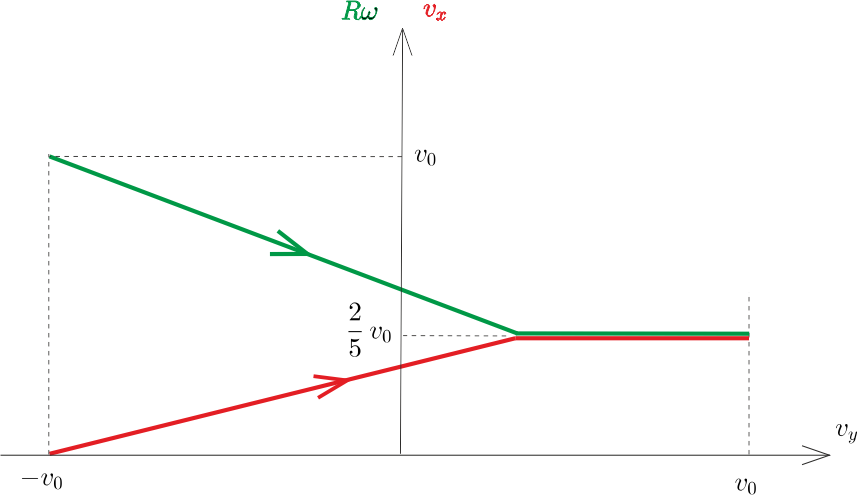
3. ábra
Ha \(\displaystyle \mu\ge \frac15\), a labda tömegközéppontjának teljes sebessége az ütközés után
\(\displaystyle v=\frac{\sqrt{29}}{5}v_0\approx 1{,}08\,v_0\)
nagyságú, és az irányának a a vízszintessel bezárt szöge
\(\displaystyle \alpha=\arctg\frac25\approx 68{,}2^\circ.\)
Ha viszont \(\displaystyle \mu\le\frac15\), akkor
\(\displaystyle v=\sqrt{1+4\mu^2}\cdot v_0\le 1{,}08\,v_0\)
és
\(\displaystyle \alpha=\arctg\frac1{2\mu}\ge\arctg\frac52\approx 68{,}2^\circ.\)
Statisztika:
26 dolgozat érkezett. 6 pontot kapott: Bencz Benedek, Csapó András, Fajszi Karsa, Hegedüs Márk, Tóth Kolos Barnabás, Zólomy Csanád Zsolt. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2023. októberi fizika feladatai

