 |
A P. 5518. feladat (2023. november) |
P. 5518. Vízszintes helyzetben rögzített, \(\displaystyle R=20\) cm sugarú, csúszós felületű hengeres testre \(\displaystyle \ell\) hosszúságú hajlékony, könnyű fonalat fektettünk az ábrán látható módon.
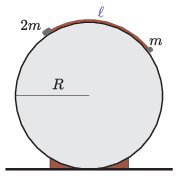
A fonál egyik végéhez \(\displaystyle m\), a másikhoz \(\displaystyle 2m\) tömegű, pontszerűnek tekinthető testet erősítettünk. Legfeljebb mekkora \(\displaystyle \ell\) esetén lehet egyensúlyban ez a rendszer?
Példatári feladat nyomán
(4 pont)
A beküldési határidő 2023. december 15-én LEJÁRT.
Megoldás. Jelöljük a két test egyensúlyi helyzetét jellemző szögeket \(\displaystyle \alpha\)-val és \(\displaystyle \beta\)-val (lásd az ábrát).
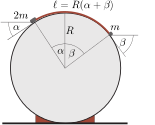
Az egyes testek akkora erőt fejtenek ki a fonálra, mintha \(\displaystyle \alpha\), illetve \(\displaystyle \beta\) hajlásszögű lejtőkön helyezkednének el. Az egyensúly feltétele:
\(\displaystyle 2mg\sin\alpha=mg\sin\beta,\)
vagyis
\(\displaystyle 2\sin\alpha=\sin\beta.\)
(Látható, hogy \(\displaystyle \alpha<\beta\).) A fonál – a kitűzési ábra szerint – mindenhol hozzáfeszül a hengerhez, tehát \(\displaystyle \beta<90^\circ\) és \(\displaystyle \alpha<90^\circ\). (Az első feltételből már következik a második.)
A szinuszfüggvény a hegyesszögek tartományában monoton növekszik, ezért nagyobb \(\displaystyle \beta\) szöghöz nagyobb \(\displaystyle \alpha\) és nagyobb \(\displaystyle R(\alpha+\beta)\) fonálhossz tartozik. A fonál leghosszabb értéke tehát a legnagyobb megengedett \(\displaystyle \beta=90^\circ\) értékhez tartozik. Ennél a szögnél
\(\displaystyle \sin\beta=1; \qquad \sin\alpha=\frac12,\)
tehát
\(\displaystyle \alpha+\beta=120^\circ=\cfrac{2\pi}{3}\ \text{rad},\)
és így
\(\displaystyle \ell_\text{max}=\frac{2\pi}{3}R\approx 42\ \rm cm.\)
Statisztika:
71 dolgozat érkezett. 4 pontot kapott: Balogh Áron , Barna Márton, Beke Botond, Bencze Mátyás, Bunford Luca, Csiszár András, Csóka Péter, Czirják Márton Pál, Dancsák Dénes, Fekete Lúcia, Flóring Balázs, Gyenes Károly, Gyerő Soma, Hegedüs Márk, Hornok Máté, Hüvös Gergely, Kallós Balázs, Kis Márton Tamás, Klement Tamás, Kovács Kristóf , Magyar Zsófia, Márfai Dóra, Papp András, Saller Bálint , Seprődi Barnabás Bendegúz, Simon János Dániel, Szabó Donát, Tóth Gellért, Tóth Hanga Katalin, Vancsisin Márk, Vásárhelyi István Péter, Veres Zsombor Gábor, Wodala Gréta Klára, Zádori Gellért, Zámbó Luca. 3 pontot kapott: Bernhardt Dávid, Bogdán Benedek, Csapó András, Dobos Anita, Erős Fanni, Fehérvári Donát, Képes Botond, Masa Barnabás, Medgyesi Júlia, Molnár Kristóf, Molnár Zétény, Szabó Imre Bence, Tárnok Ede , Tibor Varga, Vágó Botond. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2023. novemberi fizika feladatai

