 |
A P. 5519. feladat (2023. november) |
P. 5519. Dionüszosz vízszintes talajon elhelyezett egymás tetején \(\displaystyle 2\) egyforma, \(\displaystyle h\) magasságú, egyenes henger alakú, borral közel teletöltött hordót. Héraklész tizenharmadik próbájaként azt a feladatot kapja, hogy fúrjon a hordók falára merőlegesen egy-egy lyukat az alsó, illetve a felső hordóba, az adott hordó aljától mért ugyanakkora \(\displaystyle xh\) magasságban.
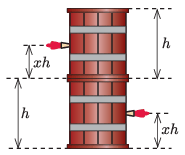
Hogyan válassza meg Héraklész a dimenziótlan \(\displaystyle x\) arányszám értékét, hogy a borsugarak földet érési pontjai a lehető legmesszebb kerüljenek egymástól?
Dürer-verseny feladata nyomán
(5 pont)
A beküldési határidő 2023. december 15-én LEJÁRT.
Megoldás. Mindkét hordónál a lyuk és a hordó teteje között \(\displaystyle h-xh=h(1-x)\) a szintkülönbség, így mindkét borsugár kiáramlási sebessége a Torricelli-törvény szerint
\(\displaystyle v=\sqrt{2gh(1-x)}.\)
Amennyiben a lyuk \(\displaystyle H\) magasan van a talaj felett, a borsugár egyes (tömegpontoknak tekinthető) darabkáinak esési ideje
\(\displaystyle T=\sqrt{\frac{2H}{g}},\)
így a borsugár a hordótól
\(\displaystyle s=vT=2\sqrt{Hh(1-x)}\)
távolságra csapódik a talajhoz. Az alsó hordónál \(\displaystyle H=xh\), tehát
\(\displaystyle s_1(x)=2h\sqrt{x(1-x)},\)
a felső hordónál pedig \(\displaystyle H=h+xh,\) így a hordótól való eltávolodása
\(\displaystyle s_2(x)=2h\sqrt{(1+x)(1-x)}.\)
A két becsapódási pont távolsága
\(\displaystyle \ell =s_1(x)+d+s_2(x)=d+2h\left(\sqrt{x(1-x)}+\sqrt{1-x^2}\right),\)
ahol \(\displaystyle d\) a hordók átmérője, hiszen a maximális távolsághoz az is kell, hogy a lyukak a hordók átellenes oldalán legyenek. Mivel \(\displaystyle h\) és \(\displaystyle d\) (\(\displaystyle x\)-től független) állandók, Héraklész feladata az
\(\displaystyle f(x)=\sqrt{x(1-x)}+\sqrt{1-x^2}\)
függvény \(\displaystyle 0<x< 1\) intervallumon felvett legnagyobb értékének, vagyis a maximumának megtalálása.
Erre hatféle módszert (!) is javasolhatunk neki. Az első egy grafikus közelítő módszer, a második felsőbb matematikát (differenciálszámítást) alkalmaz. Vannak még közelítésmentes, elemi megoldások is. A harmadik algebrai megoldás, a számtani-, a mértani- és a négyzetes közepekre vonatkozó egyenlőtlenségeket alkalmazza. A negyedik megoldási módszer lényege az \(\displaystyle f(x)\) két tagja között fennálló ,,átskálázhatósági tulajdonság'' felismerése. Ennek az eljárásnak az az érdekessége, hogy bár \(\displaystyle f(x)\) növekedési ütemére hivatkozik, de annak nagyságát (a többi módszertől eltérően) nem szükséges kiszámítanunk. Az ötödik (geometriai) módszer \(\displaystyle f(x)\) növekedési (és csökkenési) ütemét vizsgálja, de nem igényli a differenciálszámítás ismeretét. Végül a hatodik megoldási mód körök egymásba transzformálhatóságát használja.
1. módszer. Valamilyen rajzolóprogram segítségével ábrázoljuk \(\displaystyle f(x)\)-et. A grafikonról (1. ábra) leolvashatjuk, hogy a függvény a maximumát \(\displaystyle x\approx 0{,}33\approx \tfrac13\) értéknél veszi fel.
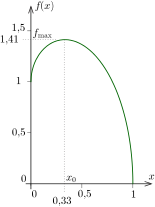
1. ábra
2. módszer. Az \(\displaystyle f(x)\) függvény maximumánál teljesül, hogy
\(\displaystyle f'(x)\equiv \frac{1-2x}{2\sqrt{x(1-x)}}- \frac{2x}{2\sqrt{1-x^2}} =0,\)
ahonnan
\(\displaystyle (1-2x)^2(1-x)(1+x)=4x^3(1-x) .\)
Mivel \(\displaystyle x<1\) (vagyis \(\displaystyle x\ne 1)\), egyszerűsíthetünk \(\displaystyle (1-x)\)-szel:
\(\displaystyle (1-2x)^2(1+x)=4x^3,\)
azaz
\(\displaystyle (1-4x+4x^2)+(x-4x^2+4x^3)=4x^3,\)
vagyis
\(\displaystyle 1-3x=0,\)
tehát a maximum helye
\(\displaystyle x_0=\frac13.\)
Behelyettesítéssel kapjuk, hogy
\(\displaystyle f_\text{max}=f(x_0)=\sqrt{\frac{2}{9}}+\sqrt{\frac{8}{9}}=\sqrt2,\)
és így
\(\displaystyle \ell_\text{max}=d+2\sqrt2 h.\)
Héraklésznek tehát a hordókat az alsó harmadrészüknél kell megfúrnia, egymással ellentétes oldalon, hogy teljesítse a próbát.
3. módszer. Bontsuk fel \(\displaystyle f(x)\)-et két tényező szorzatára:
\(\displaystyle f(x)=\sqrt{1-x}\cdot\left(\sqrt{x}+\sqrt{1+x}\right),\)
és keressünk felső korlátot a második tényezőre. Kínálja magát az ötlet, hogy a számtani közép és a négyzetes közép közötti
\(\displaystyle \frac{a+b}{2}\le \sqrt{\frac{a^2+b^2}{2}}\)
egyenlőtlenséget alkalmazzuk, hiszen ekkor a négyzetgyökök négyzete két összevonható, lineáris kifejezés lesz. Az egyenlőség csak akkor áll fenn, ha \(\displaystyle a=b\).
Esetünkben \(\displaystyle a=\sqrt{x}\) és \(\displaystyle b=\sqrt{1+x}\), ezek minden \(\displaystyle x\)-re különbözőek, az egyenlőtlenség tehát nem lehet ,,éles''.
\(\displaystyle \sqrt{x}+\sqrt{1+x}<2\sqrt{\cfrac{x+(1+x)}{2} }=2\sqrt{x+\tfrac12}.\)
Visszatérve \(\displaystyle f(x)\) felső korlátjának kereséséhez:
\(\displaystyle f(x)<2\sqrt{(1-x)\left(x+\tfrac12\right)}.\)
Itt most a mértani és a számtani közepekre vonatkozó
\(\displaystyle \sqrt{ab}\le \frac{a+b}{2}\)
egyenlőtlenséget alkalmazhatjuk:
\(\displaystyle f(x)<\frac{3}{2}.\)
Ez egy igaz állítás, de nem adja meg \(\displaystyle f(x)\) legnagyobb értékét, hiszen semmilyen \(\displaystyle x\)-nél nem éri el \(\displaystyle f(x)\) a \(\displaystyle \frac{3}{2}\) értéket.
Próbálkozhatunk azzal, hogy \(\displaystyle \sqrt{1+x}\)-et két egyenlő kifejezés összegére bontjuk:
\(\displaystyle \sqrt{1+x}=\sqrt{\tfrac14(1+x)}+\sqrt{\tfrac14(1+x)},\)
és három tagra írjuk fel a számtani és a négyzetes közepek
\(\displaystyle \frac{a+b+c}{3}\le \sqrt{\frac{a^2+b^2+c^2}{3}}\)
egyenlőtlenségét. (Az egynlőség \(\displaystyle a=b=c\) esetén teljesül.) Jelen esetben
\(\displaystyle \sqrt{x}+\sqrt{\tfrac14(1+x)}+\sqrt{\tfrac14(1+x)} \le \sqrt{3\left(x+\frac{1+x}{2} \right)}=\frac{3}{\sqrt2}\sqrt{x+\frac{1}{3}}.\)
Az egyenlőség
\(\displaystyle x=\frac{1+x}{4},\qquad\text{vagyis}\qquad x=\frac13\)
esetén teljesül.
A teljes \(\displaystyle f(x)\)-re ezt írhatjuk fel:
\(\displaystyle f(x)\equiv \sqrt{1-x}\left(\sqrt{x}+\sqrt{1+x}\right)\le \frac{3}{\sqrt2}\sqrt{1-x}\sqrt{x+\frac{1}{3}}\le \frac{3}{\sqrt2}\frac{1-x+x+\tfrac13}{2}=\sqrt{2}. \)
Ez az egyenlőtlenság \(\displaystyle 1-x=x+\tfrac13\), azaz \(\displaystyle x=\tfrac13\)-nál válik élessé, tehát ugyanott, ahol a korábbi (a négyzetes középre vonatkozó). Emiatt állíthatjuk, hogy
\(\displaystyle f(x)\le \sqrt2,\)
és az egyenlőség \(\displaystyle x=\frac13\)-nál teljesül, vagyis itt veszi fel \(\displaystyle f(x)\) a maximélis értékét.
4. módszer. Vegyük észre, hogy az
\(\displaystyle f(x)=u(x)+v(x)= \sqrt{x(1-x)}+\sqrt{(1 + x)(1-x)} \)
kifejezés két tagja lényegében azonos szerkezetű, így megfelelő ,,skálatranszformációval'' azonos alakra hozható. Ha
\(\displaystyle u(x)=\sqrt{x(1-x)}, \)
akkor
\(\displaystyle v(x)=\sqrt{(1+x)(1-x)}=2\, u(y), \qquad \text{ahol}\qquad y=\frac{1-x}{2}. \)
Valóban:
\(\displaystyle 2u(y)=2\,\sqrt{y(1-y)}=2\sqrt{\left(\frac{1-x}{2}\right)\left(1-\frac{1-x}{2}\right)}=\sqrt{(1+x)(1-x)}=v(x).\)
Ebből következően, ha az \(\displaystyle u(x)\) érintőjének a meredeksége egy \(\displaystyle x\) pontban \(\displaystyle m(x)\), tehát a függvény értéke az \(\displaystyle x+\Delta x\) pontban jó közelítéssel
\(\displaystyle u(x+\Delta x)\cong u(x)+m(x)\Delta x, \)
akkor
\(\displaystyle v(x+\Delta x)=2u\left(\frac{1-x-\Delta x}{2} \right)\cong 2 u\left(\frac {1-x}2 \right)-2\,m\left(\frac {1-x}2 \right)\frac{\Delta x}{2}, \)
és így
\(\displaystyle f(x+\Delta x)=u(x+\Delta x)+v(x+\Delta x)\cong f(x)+ m(x)\,\Delta x - m(y) \,\Delta x. \)
\(\displaystyle f(x)\)-nek ott van szélsőértéke, ahol az \(\displaystyle x\) kis változtatására az értéke nem változik. Ez nyilván teljesül abban a pontban, ahol
\(\displaystyle y=\frac{(1-x)}{2}=x ,\qquad \mbox{azaz} \qquad x=\frac{1}{3}. \)
Mivel az \(\displaystyle f(x)\)-ben a négyzetgyök alatt álló kifejezés egy lefelé nyíló parabolának felel meg, \(\displaystyle f(x)\) konkáv függvény, tehát \(\displaystyle f\)-nek csak \(\displaystyle x=\tfrac13\)-nál van szélsőértéke, és az egy maximum. Ez tehát a keresett magasság érték, és ha a hordókon a lyukak így helyezkednek el, a borsugarak becsapódási pontja között a távolság
\(\displaystyle \ell_\text{max}=d+ 2\sqrt{2}h. \)
5. módszer. \(\displaystyle f(x)\) két tag összege. Jelöljük ezeket
\(\displaystyle u(x)=\sqrt{x(1-x)}\qquad \text{és}\qquad v(x)= \sqrt{1-x^2}\)
módon, és ábrázoljuk a függvények grafikonját az \(\displaystyle (x,u)\) és \(\displaystyle (x,v)\) derékszögű koordináta-rendszerekben. Négyzetre emelés és teljes négyzetté alakítás után kapjuk, hogy
\(\displaystyle \left(x-\frac12\right)^2+u^2=\left(\frac12\right)^2,\)
illetve
\(\displaystyle x^2+v^2=1.\)
Látjuk, hogy mindkét görbe kör, pontosabban a 2. ábrán folytonos vonallal jelölt körív, hiszen
\(\displaystyle 0\le x\le 1,\quad u\ge 0 \qquad\text{és}\qquad v\ge0.\)
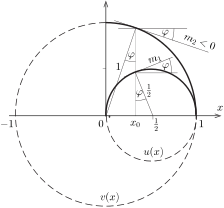
2. ábra
\(\displaystyle f(x)=u(x)+v(x)\) maximumát keressük. Legyen \(\displaystyle u(x)\) meredeksége (az érintőjének iránytangense az \(\displaystyle x\) absszciszájú helyen \(\displaystyle m_1(x)\), \(\displaystyle v(x)\) meredeksége pedig \(\displaystyle m_2(x)<0\). Keressük meg azt az \(\displaystyle x_0\) értéket, amelynél
\(\displaystyle m_1(x_0)=-m_2(x_0)=m_0,\)
vagyis \(\displaystyle f(x)\) növekedési üteme éppen nulla. A 2. ábráról leolvashatjuk, hogy egyrészt
\(\displaystyle \sin\varphi=\frac{\tfrac12-x_0}{\tfrac12}, \)
másrészt
\(\displaystyle \sin\varphi=x_0,\)
vagyis
\(\displaystyle 1-2x_0=x_0, \qquad \text{azaz}\qquad x_0=\frac13.\)
(Kihasználtuk, hogy a kisebb kör sugara \(\displaystyle 1/2\), a nagyobbé 1, és az érintők merőlegesek a körök megfelelő sugarára.)
A 2. ábráról azt is leolvashatjuk, hogy \(\displaystyle x<x_0\) esetén
\(\displaystyle m_1(x)>m_0 \qquad \text{és} \qquad m_2(x)>-m_0,\qquad \text{tehát} \qquad m_1(x)+m_2(x)>0,\)
\(\displaystyle x>x_0\) esetén pedig
\(\displaystyle m_1(x)<m_0 \qquad \text{és} \qquad m_2(x)<-m_0,\qquad \text{vagyis} \qquad m_1(x)+m_2(x)<0.\)
Ezek szerint \(\displaystyle f(x)\) monoton növekszik, amikor \(\displaystyle x<x_0\), és monoton csökken, ha \(\displaystyle x>x_0,\) tehát \(\displaystyle x_0\)-nál maximuma van.
6. módszer. Induljunk ki most is az \(\displaystyle f(x)\) függvény két tagjának megfelelő körökből. Olyan \(\displaystyle x_0\) abszcisszájú pontokat keresünk, amelyhez tartozó érintők meredekségének nagysága megegyezik, csak az előjelük különböző. A 3. ábra vázlatosan mutatja, hogy három egyszerű geometriai transzformációval a (színesen jelölt) kis kört átvihetjük (áttranszformálhatjuk) a nagyobb körbe.
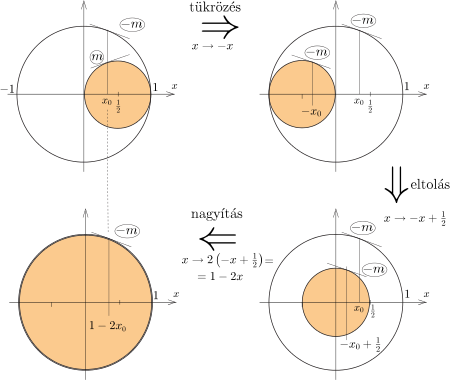
3. ábra
A tükrözés az \(\displaystyle m\) meredekséget \(\displaystyle (-m)\)-re változtatja, az eltolás és a nagyítás pedig nem változtatja meg az érintő meredekségét. Ha olyan \(\displaystyle x_0\) értéket választunk, amely a három transzformáció után éppen a kiindulási \(\displaystyle x_0\) értékkel egyezik meg, akkor megtaláltuk \(\displaystyle f(x)\) nulla meredekségű pontját, ami a keresett maximum helye.
\(\displaystyle 1-2x_0=x_0, \qquad \text{vagyis}\qquad x_0=\frac13.\)
A hordókat tehát a magasságuk alsó egyharmadánál kell megfúrni, akkor lesz legnagyobb a borsugarak becsapódási pontjai közötti távolság.
Statisztika:
75 dolgozat érkezett. 5 pontot kapott: 54 versenyző. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 4 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2023. novemberi fizika feladatai

