 |
A P. 5538. feladat (2024. január) |
P. 5538. Sok játszótéren találunk az ábrához hasonló, forgatható mászókát. Egy ilyen mászókán egy hangya mászik fel, miközben az egyenletesen forog. A felfelé kapaszkodó hangya folyamatosan azt érzi, hogy ,,függőlegesen fölfelé'' mászik.
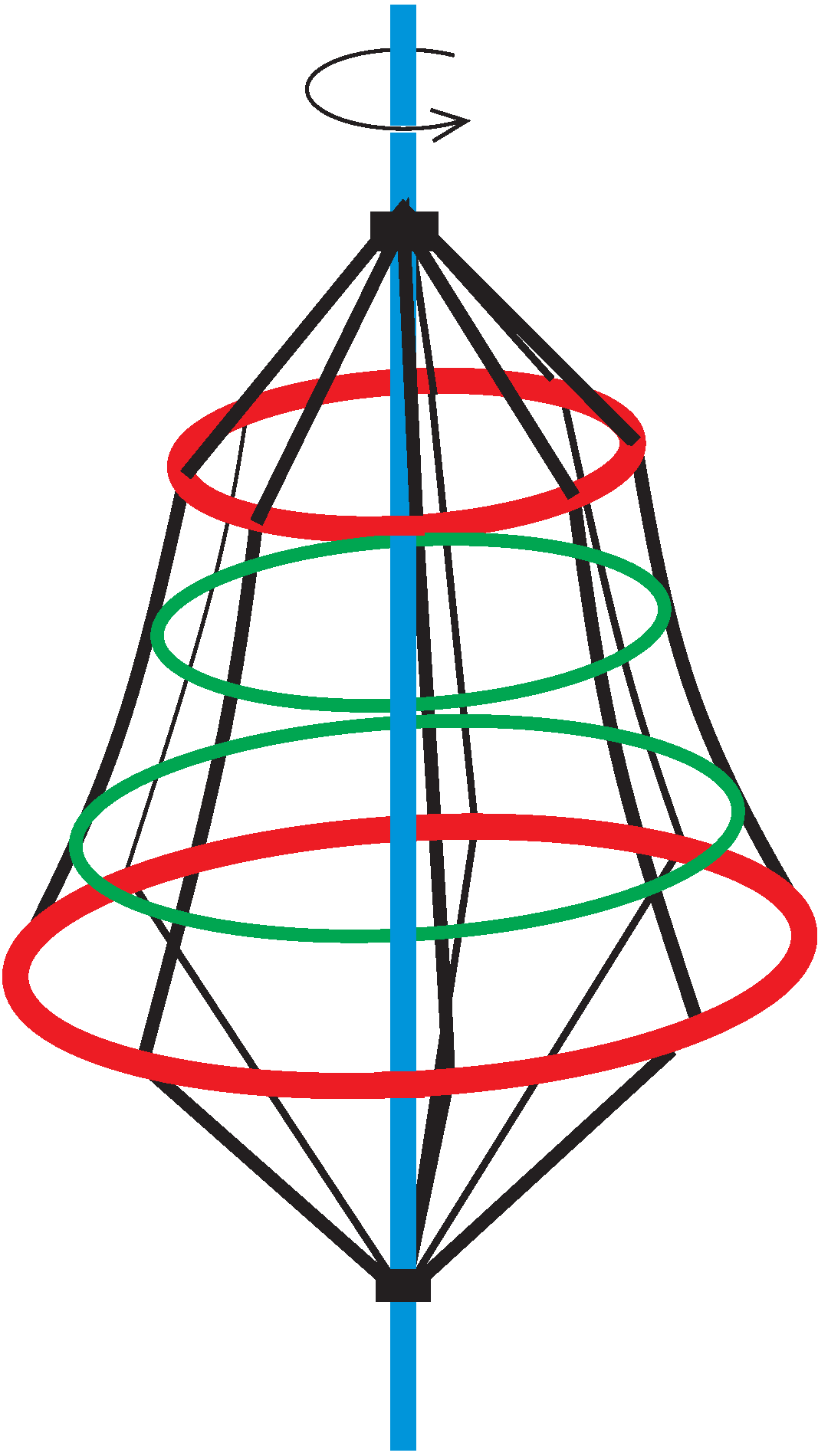
A mászóka köteleit tartó, piros körgyűrűk közül az alsó sugara \(\displaystyle 2~\text{m}\), a felsőé \(\displaystyle 1~\text{m}\), és a gyűrűk távolsága \(\displaystyle 3~\text{m}\). Mekkora fordulatszámmal forog a mászóka?
Közli: Rakovszky Andorás, Budapest
(5 pont)
A beküldési határidő 2024. február 15-én LEJÁRT.
Megoldás. Legyen az alsó merevítő gyűrű felett \(\displaystyle y\) magasságban a kötél távolsága a forgástengelytől \(\displaystyle r(y)\). Az \(\displaystyle m\) tömegű hangyára az \(\displaystyle \omega\) szögsebességgel forgó koordináta-rendszerben \(\displaystyle mg\) nagyságú, ,,valódi'' függőleges irányú nehézségi erő, valamint \(\displaystyle mr\omega^2\) nagyságú, vízszintes irányú centrifugális erő hat. Az eredő erő (a hangya által érzett nehézségi erő) párhuzamos a kötél érintőjével, tehát
\(\displaystyle \frac{mr\omega^2}{mg}=-\frac{\Delta r}{\Delta y}.\)
(\(\displaystyle \Delta r\) a forgómozgás pályasugarának kicsiny megváltozása, ha a forgástengellyel párhuzamos irányú elmozdulás egy kicsiny \(\displaystyle \Delta y\) érték.)
A fenti összefüggés szerint
\(\displaystyle \Delta r(y)=-\frac{\omega^2}{g}r(y)\cdot \Delta y.\)
Ez az egyenlet ugyanolyan alakú, mint a radioaktív bomlások \(\displaystyle \Delta m(t)=-\lambda m(t)\cdot \Delta t\) törvénye, ezért a megoldása analóg módon:
\(\displaystyle r(y)=r(0)\,\mathrm{e}^{-(\omega^2/g)y}.\)
A megadott számadatok szerint \(\displaystyle r(0)=2\,\mathrm{m}\), \(\displaystyle y=3\,\mathrm{m}\) és \(\displaystyle r(y)=1\,\mathrm{m}\), így
\(\displaystyle \omega=\sqrt{-\ln\left(\frac{r(y)}{r(0)}\right)\frac{g}{y}}=\sqrt{\ln 2\,\frac{9{,}8\,\mathrm{m/s^2}}{3\,\mathrm{m}}}=1{,}5\,\frac{1}{\mathrm{s}},\)
a fordulatszám pedig
\(\displaystyle f=\frac{\omega}{2\pi}=0{,}24\,\frac{1}{\mathrm{s}}.\)
A mászóka tehát kb. 4 másodpercenként fordul körbe.
Statisztika:
15 dolgozat érkezett. 5 pontot kapott: Czirják Márton Pál, Hegedüs Márk, Seprődi Barnabás Bendegúz. 4 pontot kapott: Csapó András, Kiss 131 Adorján Timon. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 5 versenyző.
A KöMaL 2024. januári fizika feladatai

