 Problem P. 5583. (September 2024)
Problem P. 5583. (September 2024)
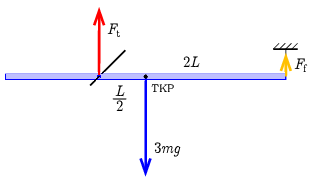
P. 5583. A thin, uniform-density rod of mass \(\displaystyle 3m\) and of length \(\displaystyle 3L\), shown in the figure, can rotate frictionlessly in a vertical plane about a horizontal axle, which is at a distance of \(\displaystyle L\) from one of the ends of the rod. The rod is held horizontal by a vertical thread attached to the other end.

\(\displaystyle a)\) What is the tension in the thread, and the force exerted on the rod by the axle, in this position?
\(\displaystyle b)\) After the thread is cut, what will the velocity of the lower endpoint of the rod be as the rod passes the vertical position?
\(\displaystyle c)\) What is the force exerted by the axle at this moment?
(4 pont)
Deadline expired on October 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. a) Az erőegyensúly és forgatónyomaték-egyensúly (a tengelyre vonatkoztatva):
$$\begin{gather*} F_\mathrm{t}+F_\mathrm{f}=3mg,\\ 3mg\frac{L}{2}=F_\mathrm{f}\cdot2L, \end{gather*}$$amiből a tengely és a fonál által kifejtett (függőlegesen felfelé mutató) erő
\(\displaystyle F_\mathrm{t}=\frac{9}{4}mg,\qquad\textrm{illetve}\qquad F_\mathrm{f}=\frac{3}{4}mg.\)
b) A mechanikai energia megmaradása alapján
\(\displaystyle 3mg\frac{L}{2}=\frac{1}{2}\Theta\omega^2,\)
ahol
\(\displaystyle \Theta=\Theta_0+3m\left(\frac{L}{2}\right)^2=\frac{1}{12}\cdot 3m\left(3L\right)^2+3m\left(\frac{L}{2}\right)^2=3mL^2.\)
Ebből a rúd szögsebessége
\(\displaystyle \omega=\sqrt{\frac{g}{L}},\)
a végpont sebessége pedig
\(\displaystyle v=2L\omega=2\sqrt{Lg}.\)
c) A legalsó helyzetben a függőleges erők eredője gyorsítja a tömegközéppontot a tengely felé:
\(\displaystyle F_\mathrm{t}'-3mg=3m\omega^2\frac{L}{2},\)
amiből a tengely által (függőlegesen felfelé) kifejtett erő:
\(\displaystyle F_\mathrm{t}'=3m\omega^2\frac{L}{2}+3mg=\frac{9}{2}mg.\)
Statistics:
79 students sent a solution. 4 points: Agócs Zoltán, Beke Márton Csaba, Bélteki Teó, Bús László Teodor, Csiszár András, Elekes Panni, Fekete Lúcia, Horvath Benedek, Kis Boglárka 08, Kovács Tamás, Misik Balázs, Monok Péter, Rózsa Laura Enikő , Szabó Márton, Szécsi Bence, Ujpál Bálint, Varga 511 Vivien, Vincze Anna. 3 points: Domján Noémi Dóra, Éliás Kristóf , Erdélyi Dominik, Gyenes Károly, Hasulyó Dorián, Kiss 131 Adorján Timon, Klement Tamás, Magyar Zsófia, Nagy Gellért Ákos, Papp Emese Petra, Simon János Dániel, Tóth Hanga Katalin. 2 points: 28 students. 1 point: 7 students. 0 point: 3 students. Not shown because of missing birth date or parental permission: 1 solutions.
Problems in Physics of KöMaL, September 2024
