Problem P. 5584. (September 2024)

P. 5584. Place a closed loop of thread on a soap-film formed on a frame, which was dipped in soapy water. Then pierce the centre of the loop with a pin. The thread loop is stretched into a circle. Determine the tension in the circular thread as a function of the radius of the circle and the surface tension.

(4 pont)

Deadline expired on October 15, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelöljük a szappanos víz felületi feszültségét \(\displaystyle \alpha\)-val. Ekkor a szappanhártya egységnyi hosszúságú darabjára annak határán (a hártya 2 oldalát is figyelembe véve) \(\displaystyle 2\alpha\) nagyságú, a határgörbe érintőjére merőleges erő hat.

Tekintsük a cérnahurok gondolatban kettévágott, a \(\displaystyle 2r\) hosszúságú vágás mentén egy merev pálcikával lezárt részét. Az elvágott fonál két végén ható, összesen \(\displaystyle 2F\) nagyságú erő tart egyensúlyt a hártyának a félkör mentén kifejtett húzóerejével (lásd az ábra bal oldali felét).

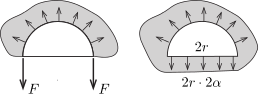
Ha a kör átmérője mentén elhelyezkedő, \(\displaystyle 2r\) hosszúságú pálca másik oldalán is szappanhártya feszülne, az összesen \(\displaystyle 2r\cdot 2\alpha\) erőt fejtene ki, és a zárt félkör a határán ható (a felületi feszültségből származó) erők hatására egyensúlyban maradna (lásd az ábra jobb oldali felét).

A két elrendezést összevetve mondhatjuk, hogy

\(\displaystyle 2F=2r\cdot 2\alpha,\)

vagyis a fonalat feszítő erő

\(\displaystyle F=2r\alpha.\)

Statistics:

27 students sent a solution.
4 points:	Agócs Zoltán, Bélteki Teó, Horvath Benedek, Klement Tamás, Masa Barnabás, Papp András, Ujpál Bálint.
3 points:	Csiszár András, Zádori Gellért.
2 points:	11 students.
1 point:	2 students.
0 point:	1 student.

Problems in Physics of KöMaL, September 2024