Problem P. 5588. (September 2024)

P. 5588. A thin insulating ring of radius \(\displaystyle R\), uniformly charged with \(\displaystyle {+Q}\), is placed in a horizontal plane. Along the diameter of the fixed ring (e.g. along a stretched fishing line), a point-like body with a charge \(\displaystyle {+q}\) and mass \(\displaystyle m\) can move frictionlessly. The point-like body is slightly displaced from its equilibrium position. What is the period of the small oscillations that occur?

(6 pont)

Deadline expired on October 15, 2024.

Sorry, the solution is available only in Hungarian. Google translation

I. megoldás. Határozzuk meg, hogy milyen elektromos mezőt hoz létre önmagában a töltött szigetelő gyűrű a középpontjának kicsiny környezetében. Ha azt kapjuk, hogy a gyűrű átmérője mentén az elektromos térerősség (jó közelítéssel) arányos a középponttól mért távolsággal, akkor már könnyen megadhatjuk a pontszerű, töltött test periodikus mozgásának rezgésidejét.

Válasszunk egy olyan koordináta-rendszert, amelynek origója a gyűrű középpontja, \(\displaystyle z\) tengelye pedig a gyűrű síkjára merőleges szimmetriatengely. Ezen a tengelyen az origótól \(\displaystyle z_0\ll R\) távol lévő pontban a hengerszimmetria miatt az elektromos térerősség nyilván \(\displaystyle z\) irányú, nagysága pedig jó közelítéssel

\(\displaystyle E_z(z_0)=k\frac{Q}{R^3}\,z_0.\)

Ezt úgy láthatjuk be, hogy felosztjuk a gyűrűt sok kicsi, egyenként \(\displaystyle \Delta Q\) töltésű darabkára (1. ábra), és ezek elektromos térerősségvektorait összegezzük.

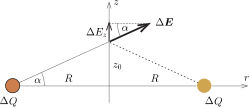
1. ábra

Az egyes darabok járuléka az elektromos mezőhöz \(\displaystyle \vert{\Delta\boldsymbol E}\vert=k\frac{\Delta Q}{R^2+z_0^2}\) nagyságú, a térerősségvektor \(\displaystyle z\) tengely irányú komponense pedig \(\displaystyle \vert{\Delta\boldsymbol E}\vert\)-nek \(\displaystyle \sin\alpha=z_0/\sqrt{R^2+z_0^2}\)-szerese:

\(\displaystyle \Delta E_z(z_0)=k\frac{\Delta Q}{\left(R^2+z_0^2\right)^{3/2}}z_0\approx k\frac{\Delta Q}{R^3}z_0.\)

(A nevezőben \(\displaystyle z_0^2\)-t elhanyagoltuk \(\displaystyle R^2\) mellett, hiszen \(\displaystyle z_0\ll R\). A képlet végén szereplő \(\displaystyle z_0\) mennyiséget természetesen nem hanyagolhatjuk el, mert nincs mellette egy másik távolság, amihez képest nagyon kicsi lenne.)

A teljes gyűrű (\(\displaystyle z\) irányú) elektromos terének (előjeles) nagysága, vagyis a \(\displaystyle z\) komponense:

\(\displaystyle E_z(z_0)=\sum k\frac{\Delta Q}{R^3}z_0=k\frac{z_0}{R^3}\sum\Delta Q=k\frac{Q}{R^3}z_0.\)

Helyezzünk el – gondolatban – a gyűrű középpontjánál egy kicsiny hengert, amelynek alapköre \(\displaystyle r_0\) sugarú, a magassága \(\displaystyle 2z_0\), és a szimmetriatengelye a \(\displaystyle z\) tengely (2. ábra). A hengerben nincsenek töltések, így – a Gauss-féle fluxustörvény szerint – a teljes felületén áthaladó \(\displaystyle \Psi\) elektromos fluxus nulla.

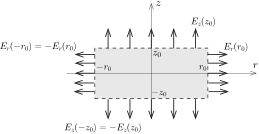
2. ábra

A henger két körlapján összesen

\(\displaystyle \Psi_1=2E_z(z_0)\cdot r_0^2\pi\)

fluxus távozik a hengerből. (Ez a megállapítás csak közelítőleg igaz, hiszen a körlapok mentén a térerősség \(\displaystyle z\) komponensét ugyanakkorának veszi, mint amennyi az a szimmetriatengelyen, holott \(\displaystyle E_z\) \(\displaystyle z_0\)-n kívül nyilván a tengelytől mért \(\displaystyle r\) távolságtól is függhet. Ezt a függést azonban \(\displaystyle r\le r_0\ll R\) miatt elhanyagolhatjuk, mert a fluxushoz csak \(\displaystyle z_0\) vagy \(\displaystyle r_0\) szorzatával (esetleg magasabb hatványaikkal) arányos, tehát nagyon kicsiny járulékot ad.)

A henger palástján keresztül kilépő fluxus

\(\displaystyle \Psi_2=E_r(r_0)\cdot 2\pi r_0\cdot 2z_0.\)

(Ez az összefüggés is tartalmaz közelítést, mert elhanyagolja, hogy \(\displaystyle E_r(r)\) nemcsak \(\displaystyle r_0\)-tól, hanem \(\displaystyle z\)-től is függhet. Ez a függés azonban \(\displaystyle z_0\ll R\) miatt ugyancsak ,,másodrendűen kicsi'' korrekciót eredményez a fluxus kiszámításánál.)

A teljes elektromos fluxus \(\displaystyle \Psi_1+\Psi_2=0\), vagyis

\(\displaystyle 2k\frac{Q}{R^3}z_0\cdot r_0^2\pi+E_r(r_0)\cdot 2\pi r_0\cdot 2z_0=0.\)

Innen leolvasható, hogy

\(\displaystyle E_r(r_0)=-k\frac{Q}{2R^3}\,r_0.\)

Ennek megfelelően a horgászzsinóron csúszkáló, \(\displaystyle q\) töltésű pontszerű testre ható erő az origótól \(\displaystyle r\) távolságban

\(\displaystyle F(r)=-k\frac{qQ}{2R^3}\,r\equiv -D\cdot r.\)

(A negatív előjel arra utal, hogy az erő az egyensúlyi helyzet felé mutató vektor, tehát \(\displaystyle r=0\) stabil egyensúlyi helyzet.)

A fenti erőtörvény éppen olyan, mint egy \(\displaystyle D\) direkciós erejű rugónál, a kialakuló mozgás periódusideje tehát

\(\displaystyle T=2\pi\sqrt{\frac{m}{D}}=2\pi\sqrt{\frac{2mR^3}{kqQ}}.\)

Megjegyzés. Az alkalmazott közelítések alapja az, hogy az elrendezés a \(\displaystyle z\) tengelyre nézve forgásszimmetrikus, a gyűrű síkjára nézve pedig tükörszimmetrikus. Tekintsük pl. a térerősséget egy a szimmetriasíktól \(\displaystyle z\), a forgástengelytől \(\displaystyle r\) távolságra levő pontban! A gyűrű síkjára való tükrözéskor a radiális komponens nem változhat, tehát \(\displaystyle z\)-nek csak páros hatványitól függhet, míg a síkra merőleges komponensnek előjelet kell váltania, tehát \(\displaystyle z\) páratlan függvénye. Ennek megfelelően egy a \(\displaystyle z\) tengellyel párhuzamos egyenes mentén a radiális komponensnek szélsőértéke (maximuma) van a gyűrű síkjában, és ettől távolodva az értéke csak \(\displaystyle z\) négyzetével vagy annál lassabban változhat. Mivel bármely sík, ami a forgástengelyt tartalmazza, maga tükörsík, gondolatmenetünket egy ilyen síkra megismételve azt találjuk, hogy a térerősség \(\displaystyle z\) irányú komponense a \(\displaystyle z\) tengelytől mért \(\displaystyle r\) távolság páros függvénye lehet csak, így a tengely közelében csak lassan, legfeljebb \(\displaystyle r^2\)-tel arányosan változhat.

Összefoglalva: Az elektromos térerősség hengerkoordináta-rendszerbeli komponensei az origó közelében így írhatók fel:

\(\displaystyle E_r(r,z)=a_1r+a_2rz^2+\cdots\approx a_1r,\)

\(\displaystyle E_z(r,z)=b_1z+b_2zr^2+\cdots\approx b_1z.\)

Látható, hogy abban a közelítésben, hogy \(\displaystyle r\) és \(\displaystyle z\) 1-nél magasabb kitevőjű hatványai elhanyagoljuk, \(\displaystyle E_z\) nem függ \(\displaystyle r\)-től és arányos \(\displaystyle z\)-vel, \(\displaystyle E_r\) pedig \(\displaystyle z\)-től független és \(\displaystyle r\)-rel arányos.

II. megoldás. Az \(\displaystyle E_r(r)\) térerősséget, kicsit több munka árán, direkt módon is kiszámíthatjuk. Osszuk fel a gyűrűt \(\displaystyle R\Delta\varphi\) hosszúságú kicsiny ívekre, és számoljuk ki ezen darabok járulékát a gyűrű síkjában fekvő, a forgástengelytől \(\displaystyle r\) távolságra levő \(\displaystyle P\) pontban! (A jelöléseket a 3. ábra mutatja.)

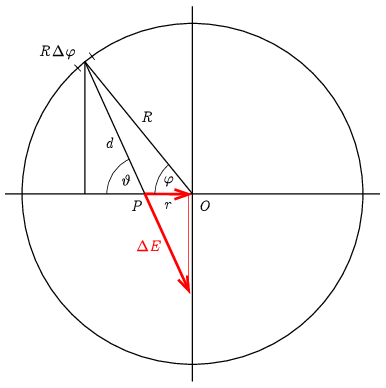
3. ábra

A bejelölt \(\displaystyle R\Delta\varphi\) hosszúságú szakasz \(\displaystyle \Delta Q=\Delta\varphi(Q/2\pi)\) töltése által létrehozott térerősség \(\displaystyle OP\) irányú komponensének a nagysága a \(\displaystyle P\) pontban

\(\displaystyle \Delta E_r=\Delta E\cos\vartheta=-k\frac{\Delta Q}{d^2}\cos\vartheta.\)

(A járulék erre merőleges komponensével nem kell számolnunk, mert az az összegzés során a szimmetria miatt kiesik.) A koszinusztétel segítségével

\(\displaystyle d=\sqrt{R^2+r^2-2Rr\cos\varphi}\qquad\textrm{és}\qquad\cos\vartheta=\frac{R\cos\varphi-r}{d}=\frac{R\cos\varphi-r}{\sqrt{R^2+r^2-2Rr\cos\varphi}},\)

így

\(\displaystyle \Delta E_r=-k\Delta Q\frac{R\cos\varphi-r}{\left(\sqrt{R^2+r^2-2Rr\cos\varphi}\right)^3},\)

ami \(\displaystyle R\) kiemelése után

\(\displaystyle \Delta E_r=-\frac{k\Delta Q}{R^2}\frac{\cos\varphi-(r/R)}{\left(\sqrt{1+(r/R)^2-2(r/R)\cos\varphi}\right)^3}.\)

alakú. Feltételezésünk szerint \(\displaystyle r\ll R\), így alkalmazhatjuk az \(\displaystyle \vert x\vert\ll 1\) értékekre érvényes \(\displaystyle (1+x)^{-n/m}\approx (1-nx/m)\) közelítést, és az \(\displaystyle (r/R)^2\)-tel arányos tagokat az egy nagyságrendű tagok mellett elhanyagolhatjuk. Így a

\(\displaystyle \Delta E_r=-\frac{k\Delta Q}{R^2}\left(\cos\varphi+\frac{r}{R}\left(3\cos^2\varphi-1\right)\right)=-\frac{k\Delta Q}{R^2}\left(\cos\varphi+\frac{r}{R}\left(\frac{1}{2}+\frac{3}{2}\cos(2\varphi)\right)\right)\)

kifejezésre jutunk. Ezt és \(\displaystyle \Delta Q\) értékét felhasználva

\(\displaystyle E_r(r)=-\frac{kQ}{R^2}\frac{1}{2\pi}\sum\left(\cos\varphi+\frac{r}{R}\left(\frac{1}{2}+\frac{3}{2}\cos(2\varphi)\right)\right)\Delta\varphi.\)

Mivel a teljes \(\displaystyle 0\le\varphi\le2\pi\) tartományra nézve mind \(\displaystyle \sum\cos\varphi\Delta\varphi\), mind pedig \(\displaystyle \sum\cos(2\varphi)\Delta\varphi\) nulla, viszont \(\displaystyle \sum\Delta\varphi=2\pi\),

\(\displaystyle E_r(r)=-\frac{kQ}{2R^3}r.\)

A horgászzsinóron csúszkáló pontszerű testre ható erő az origótól \(\displaystyle r\) távolságban

\(\displaystyle F(r)=-k\frac{qQ}{2R^3}\,r\equiv -D\cdot r.\)

A kialakuló mozgás harmonikus rezgőmozgás, amelynek rezgésideje

\(\displaystyle T=2\pi\sqrt{\frac{m}{D}}=2\pi\sqrt{\frac{2mR^3}{kqQ}}.\)

Statistics:

19 students sent a solution.
6 points:	Beke Márton Csaba, Bencz Benedek, Gyenes Károly, Kiss 131 Adorján Timon, Simon János Dániel, Tóth Kolos Barnabás.
5 points:	Csiszár András.
4 points:	2 students.
3 points:	3 students.
1 point:	2 students.
Unfair, not evaluated:	2 solutionss.

Problems in Physics of KöMaL, September 2024