 Problem P. 5591. (October 2024)
Problem P. 5591. (October 2024)
P. 5591. We make three different compound pendulums (physical pendulums).
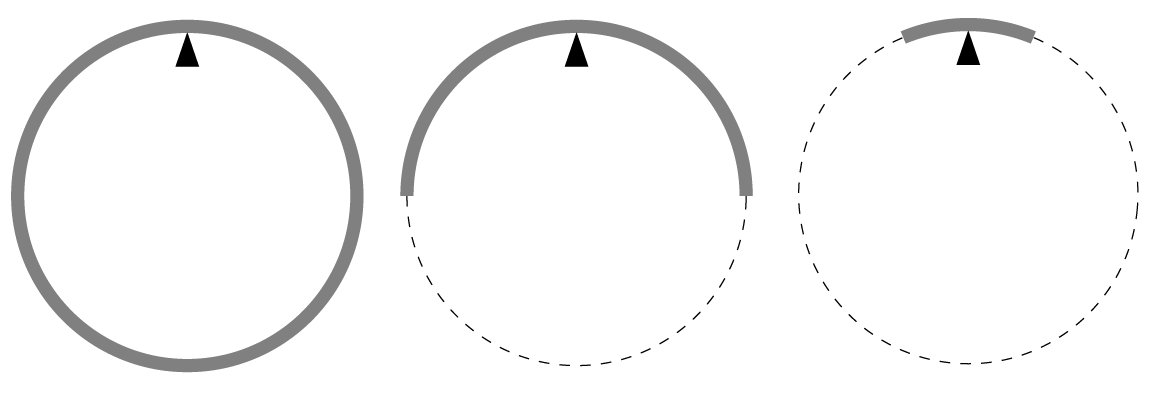
\(\displaystyle a)\) A thin rod with uniform mass distribution is bent into a circle of radius \(\displaystyle R\), and is supported by a wedge at a point on the inner rim of the circle, see the figure. The circular rod is free to rotate about the wedge in its plane.
\(\displaystyle b)\) A semicircle is cut from a similarly bent rod forming a circle of the same radius. This semicircular rod is supported at the midpoint of its circumference.
\(\displaystyle c)\) The same procedure is followed as in the previous case, but only a relatively short arc, an octant of the circular arc is placed at its midpoint to the wedge.
All three pendulums are slightly displaced and the periods of their swings are measured. Which of these periods will be the greatest and which will be the smallest?
(5 pont)
Deadline expired on November 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük a kör középpontját \(\displaystyle O\)-val, a belőle kivágott ív tömegét \(\displaystyle m\)-mel, az \(\displaystyle S\) tömegközéppont és a \(\displaystyle P\) alátámasztási pont távolságát pedig \(\displaystyle s\)-sel. (\(\displaystyle s\) függ a körív ,,nyílásszögétől''.) A fizikai inga lengésidő-képlete szerint
\(\displaystyle T=2\pi\sqrt{\frac{\Theta_P}{mgs}},\)
ahol \(\displaystyle \Theta_P\) a körívnek a \(\displaystyle P\) pontra vonatkoztatott tehetetlenségi nyomatéka.
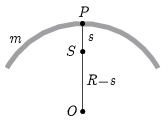
Számítsuk ki \(\displaystyle \Theta_P\)-t a Steiner-tétel felhasználásával! Nyilván \(\displaystyle \Theta_O=mR^2\), hiszen az ív minden pontja \(\displaystyle R\) távol van a kör középpontjától. Alkalmazzuk a Steiner-tételt a \(\displaystyle P\) pontra és az \(\displaystyle O\) pontra:
\(\displaystyle \Theta_P=\Theta_S+ms^2,\)
\(\displaystyle \Theta_O=\Theta_S+m(R-s)^2.\)
A két egyenlet különbségéből \(\displaystyle \Theta_S\) kiesik:
\(\displaystyle \Theta_P-mR^2=ms^2-m(R-s)^2,\)
vagyis
\(\displaystyle \Theta_P=2mRs,\)
a lengésidő tehát
\(\displaystyle T=2\pi\sqrt{\frac{\Theta_P}{mgs}}=2\pi\sqrt{\frac{2R}{g}}.\)
Meglepő módon a lengésidő nem függ \(\displaystyle s\)-től, vagyis nem függ a körív nyílásszögétől. A feltett kérdésekre tehát az a válasz, hogy mindhárom alakzat lengésideje (kis kitérések esetén) ugyanakkora.
Statistics:
28 students sent a solution. 5 points: Agócs Zoltán, Beke Márton Csaba, Erdélyi Dominik, Gyenes Károly, Simon János Dániel, Tóth Hanga Katalin. 4 points: Csiszár András, Horváth 001 Botond , Ujpál Bálint. 3 points: 4 students. 2 points: 5 students. 1 point: 5 students. 0 point: 3 students.
Problems in Physics of KöMaL, October 2024
