 Problem P. 5593. (October 2024)
Problem P. 5593. (October 2024)
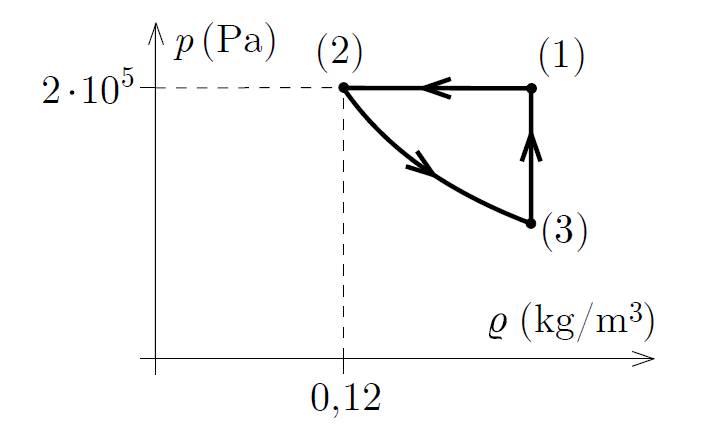
P. 5593. A heat engine is operated with a sample of helium, which has a constant amount. The pressure-density graph of the different parts of the cyclical process is shown in the figure. The temperature of the gas in its initial state (1) is 400 K, and during the process between states (2) and (3) the product of the pressure and the density of the gas is constant.
\(\displaystyle a)\) What is the temperature of the gas at state (2) and at state (3)?
\(\displaystyle b)\) What is the efficiency of this heat engine?
(5 pont)
Deadline expired on November 15, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. a) Az ideális gáz állapotegyenlete:
\(\displaystyle pV=\frac{mRT}{M}\quad\rightarrow\quad p=\frac{\varrho RT}{M},\)
ahol \(\displaystyle R=8{,}314\,\mathrm{\tfrac{J}{mol\,K}}\), \(\displaystyle M=0{,}004\,\mathrm{\tfrac{kg}{mol}}\), és így \(\displaystyle \tfrac{M}{R}=0{,}000481\,\mathrm{\tfrac{kg\,K}{J}}\). Ebből
$$\begin{align*} \varrho_1&=\frac{p_1}{T_1}\cdot\frac{M}{R}\approx 0{,}24\,\mathrm{\frac{kg}{m^3}}\\ T_2&=\frac{p_2}{\varrho_2}\cdot\frac{M}{R}\approx 800\,\mathrm{K}. \end{align*}$$A (3)\(\displaystyle \rightarrow\)(1) folyamatban a sűrűség állandó, így
\(\displaystyle \varrho_3=\varrho_1\approx 0{,}24\,\mathrm{\frac{kg}{m^3}}.\)
A (2)\(\displaystyle \rightarrow\)(3) folyamatban \(\displaystyle p\varrho=\textrm{állandó}\), így
\(\displaystyle p_3=\frac{p_2\varrho_2}{\varrho_3}\approx 100\,\mathrm{kPa}.\)
Ezekből, ismét az állapotegyenletet használva
\(\displaystyle T_3=\frac{p_3}{\varrho_3}\cdot\frac{M}{R}\approx 200\,\mathrm{K}.\)
A gáz állapotjelzőit a folyamat megjelölt pontjain az 1. táblázatban foglaltuk össze.
1. táblázat
b) Rajzoljuk át a folyamatot a \(\displaystyle p\,\)-\(\displaystyle V\) állapotsíkra (ábra)!
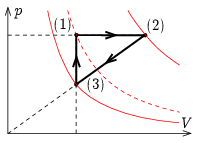
Az (1)\(\displaystyle \rightarrow\)(2) folyamatban a nyomás állandó, a sűrűség csökken, így a térfogat nő, tehát ez egy izobár tágulás. A (2)\(\displaystyle \rightarrow\)(3) folyamatban a \(\displaystyle p\varrho\) szorzat állandóságából következően a \(\displaystyle \tfrac{p}{V}\) hányados állandó, azaz a folyamat a \(\displaystyle p\,\)-\(\displaystyle V\) állapotsíkon egy origón átmenő egyenesre illeszkedő szakasz. Végül a (3)\(\displaystyle \rightarrow\)(1) folyamatban a sűrűség állandóságából következtetően a térfogat is állandó, ez egy izochor folyamat.
Az ábrára berajzoltuk a (3)-as és (2)-es állapoton (folytonos piros vonallal), valamint a köztes, (1)-es állapoton (szaggatott piros vonallal) áthaladó adiabatákat. Láthatjuk, hogy a gáz a (3)\(\displaystyle \rightarrow\)(1) és (1)\(\displaystyle \rightarrow\)(2) folyamatban hőt vesz fel, a (2)\(\displaystyle \rightarrow\)(3) folyamatban pedig hőt ad le.
A (3)\(\displaystyle \rightarrow\)(1) izochor folyamatban a hőfelvétel
\(\displaystyle Q_{\textrm{fel},3\rightarrow 1}=\frac{3}{2}nR(T_1-T_3)=300\,\mathrm{K}\cdot nR,\)
az (1)\(\displaystyle \rightarrow\)(2) izobár folyamatban a hőfelvétel
\(\displaystyle Q_{\textrm{fel},1\rightarrow 2}=\frac{5}{2}nR(T_2-T_1)=1000\,\mathrm{K}\cdot nR.\)
A teljes körfolyamat alatt a gáz munkavégzése a \(\displaystyle p\,\)-\(\displaystyle V\) állapotsíkon a körfolyamat által körbezárt terület nagysága:
\(\displaystyle W_\mathrm{g}=\frac{1}{2}(p_1-p_3)(V_2-V_1)=\frac{nR}{2}(p_1-p_3)\left(\frac{T_2}{p_2}-\frac{T_1}{p_1}\right)=100\,\mathrm{K}\cdot nR.\)
Ez alapján a hőerőgép hatásfoka
\(\displaystyle \eta=\frac{W_\mathrm{g}}{Q_\mathrm{fel}}=\frac{100\,\mathrm{K}\cdot nR}{1300\,\mathrm{K}\cdot nR}=\frac{1}{13}\approx 7{,}7\%.\)
A folyamatok jellemzőit a 2. táblázatban foglaltuk össze.
2. táblázat
Megjegyzés. A hatásfokot azért nem lehet a Carnot-folyamatból ismert \(\displaystyle \eta=\tfrac{T_\mathrm{max}-T_\mathrm{min}}{T_\mathrm{max}}\) összefüggéssel számolni, mert ez nem egy Carnot-körfolyamat, esetünkben a hőfelvétel közben a gáz hőmérséklete – a Carnot-folyamattal ellentétben – folyamatosan változik, és így a hőcseréhez (elvileg) végtelen sok hőtartályra lenne szükség, hiszen reverzibilis hőátadás csak (majdnem) azonos hőmérsékletű hőtartályok között lehetséges. Ha a hőfelvétel végig egy \(\displaystyle T_\mathrm{max}=800\,\mathrm{K}\)-es ,,felső'' és egy \(\displaystyle T_\mathrm{min}=200\,\mathrm{K}\)-es ,,alsó'' hőtartályhoz kapcsolva történik, akkor a hőátadás irreverzibilis lesz, és így az entrópia nem marad állandó (növekszik), a hatásfok pedig rosszabb lesz, mint az ekkora hőmérsékletek között működő Carnot-gépé.
A gyakorlatban a sok hőtartály helyett például ellenáramlásos hőátadást használnak: a hideg gázt kezdetben a felmelegedett hűtőközeg melegíti (ahogyan a modern kéményekben a beáramló hideg levegőt a kiáramló forró égéstermék), és ezzel a hatásfok javítható. Természetesen az elvi határt jelentő Carnot-hatásfokot nem lehet túllépni.
Statistics:
46 students sent a solution. 5 points: Agócs Zoltán, Csiszár András, Erdélyi Dominik, Fekete Lúcia, Gyenes Károly, Hornok Máté, Horvath Benedek, Klement Tamás, Kovács Tamás, Sütő Áron, Tóth Hanga Katalin, Vértesi Janka, Zólomy Csanád Zsolt. 4 points: Tóthpál-Demeter Márk. 3 points: 9 students. 2 points: 6 students. 1 point: 8 students. 0 point: 1 student. Not shown because of missing birth date or parental permission: 1 solutions.
Problems in Physics of KöMaL, October 2024
