Problem P. 5595. (October 2024)

P. 5595. Two concave mirrors with small aperture angles and with focal length of \(\displaystyle f\) are placed opposite to each other so that their principal axes coincide and their distance from each other is \(\displaystyle 2f\) (see figure).

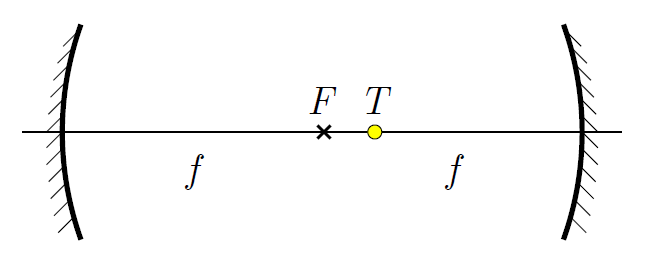
A point-like light source is placed at a point \(\displaystyle T\) on the principal axis. Where is the position of point \(\displaystyle T\) if the emitted light rays meet at point \(\displaystyle T\) after they are reflected from the two mirrors?

(4 pont)

Deadline expired on November 15, 2024.

Sorry, the solution is available only in Hungarian. Google translation

I. megoldás. Az első leképzésnél a tárgytávolság (a \(\displaystyle T\) pont és az egyik tükör távolsága) legyen \(\displaystyle t_1\). Ekkor az első tükröződés után keletkező kép \(\displaystyle k_1\) távolsága a leképzési törvény \(\displaystyle \left(\tfrac{1}{f}=\tfrac{1}{t}+\tfrac{1}{k}\right)\) alapján:

\(\displaystyle k_1=\frac{ft_1}{t_1-f}.\)

Az első kép távolsága a másik tükörtől (\(\displaystyle t_2\)):

\(\displaystyle t_2=2f-k_1=\frac{f(t_1-2f)}{t_1-f},\)

és ebből a \(\displaystyle k_2\) második képtávolság:

\(\displaystyle k_2=\frac{ft_2}{t_2-f}=2f-t_1.\)

Azaz a második leképzés után a kép a \(\displaystyle t_1\) távolságtól függetlenül a \(\displaystyle T\) pontra esik, a fényforrás tehát bárhol lehet.

Megjegyzés. Ha \(\displaystyle t_1>f\), akkor az első kép valódi lenne, de a másik tükör mögé esik, így a második leképzésnek egy virtuális tárgya van (1. ábra). Ha \(\displaystyle t_1<f\), akkor az első leképzésnél látszólagos kép keletkezik, ezt képezi le a második visszaverődés (2. ábra). A második leképzés után viszont mindenképp valódi képet kapunk, és a végső nagyítás minden esetben \(\displaystyle N=N_1N_2=\tfrac{k_1}{t_1}\,\tfrac{k_2}{t_2}=-1\) lesz, tehát a kép mérete megegyezik a tárgyéval, de fordított állású lesz.

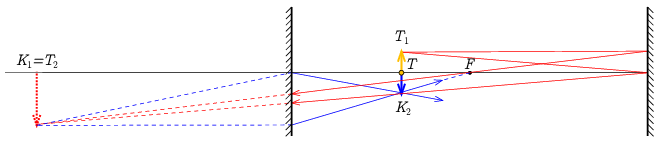
1. ábra

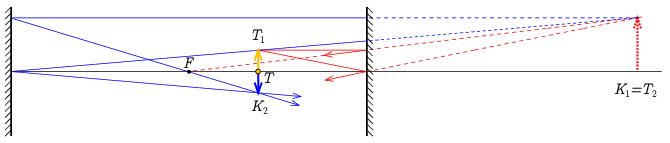
2. ábra

\(\displaystyle t_1=f\) esetében nem keletkezik az első tükröződés után kép, a fókuszsíkból induló fénysugarak a tükörről párhuzamosan verődnek vissza, amelyeket a másik tükör ismét a fókuszsíkba gyűjt, tehát ilyenkor is teljesül, hogy a fénysugarak kétszeres visszaverődés után a \(\displaystyle T\) ponton mennek át (3. ábra).

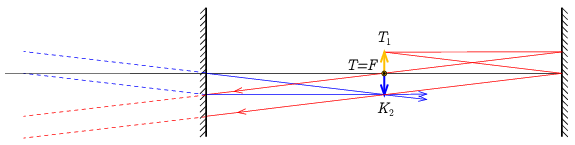
3. ábra

(Az ábrákon a fény először a jobb oldali, aztán a bal oldali tükrön tükröződik, de ennek az elrendezés szimmetriája miatt nincs jelentősége.)

II. megoldás. Még egyszerűbben jutunk az eredményre, ha a leképzési törvény Newton-féle alakját használjuk (lásd a G. 855. gyakorlatot a 2024.  évi májusi számában és a megoldását a munkafüzetben). Ekkor a ,,fókuszontúli'' tárgy- és képtávolság \(\displaystyle x_\mathrm{t}=t-f\), illetve \(\displaystyle x_\mathrm{k}=k-f\), és ezekre teljesül az \(\displaystyle x_\mathrm{t}x_\mathrm{k}=f^2\) összefüggés. Esetünkben ez azt jelenti, hogy az \(\displaystyle x_\mathrm{t}\) és \(\displaystyle x_\mathrm{k}\) távolságokat a közös fókuszponttól kell mérni, és így \(\displaystyle x_\mathrm{t2}=-x_\mathrm{k1}\), amiből azonnal \(\displaystyle x_\mathrm{k2}=-x_\mathrm{t1}\) következik bármely \(\displaystyle x_\mathrm{t1}\) esetében.

Statistics:

29 students sent a solution.
4 points:	Blaskovics Ádám.
3 points:	Bense Tamás, Bús László Teodor, Csiszár András, Kis Boglárka 08, Tóth-Tűri Bence, Vincze Anna.
2 points:	3 students.
1 point:	7 students.
0 point:	2 students.
Unfair, not evaluated:	2 solutionss.
Not shown because of missing birth date or parental permission:	2 solutions.

Problems in Physics of KöMaL, October 2024