 Problem P. 5607. (December 2024)
Problem P. 5607. (December 2024)
P. 5607. A small body is projected horizontally from the top of a fixed slope, and hits the bottom of the slope (see the figure). On impact, its velocity makes an angle of \(\displaystyle \beta=19^\circ\) with the plane of the slope. What is the angle of inclination of the slope?
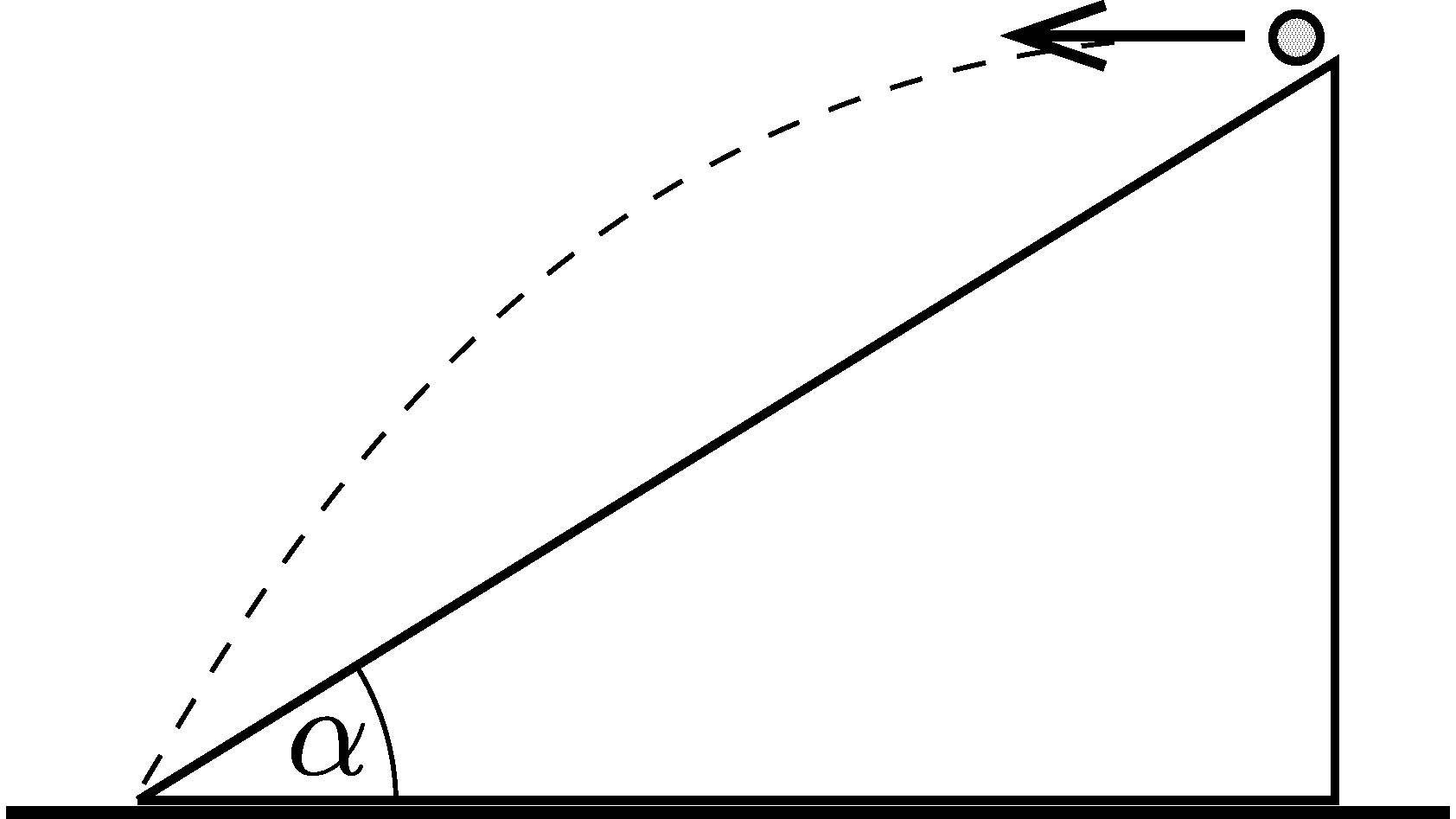
(3 pont)
Deadline expired on January 15, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük a lejtő alapjának hosszát \(\displaystyle d\)-vel, a lejtő magassága ekkor \(\displaystyle h=d\tg\alpha\). A függőleges mozgás \(\displaystyle h\) magasságból induló szabadesés, az ideje tehát
\(\displaystyle t=\sqrt{\frac{2d\tg\alpha}{g}}.\)
A becsapódáskor a test függőleges irányú sebessége
\(\displaystyle v_y=gt=\sqrt{2gd\tg\alpha}.\)
A test vízszintes irányban egyenletesen mozog, a sebessége
\(\displaystyle v_x=\frac{d}{t}=\sqrt{\frac{gd}{2\tg\alpha}}.\)
A becsapódáskor a test sebessége a vízszintessel \(\displaystyle \alpha+\beta\) szöget zár be, fennáll tehát
\(\displaystyle \tg(\alpha+\beta)=\frac{\tg\alpha+\tg\beta}{1-\tg\alpha\cdot\tg\beta}=\frac{v_y}{v_x}=2\tg\alpha.\)
A fentebbi egyenlet így is felírható:
\(\displaystyle 2\tg\beta\cdot\tg^2\alpha-\tg\alpha+\tg\beta=0,\)
ami az \(\displaystyle X\equiv\tg\alpha\) változóra nézve másodfokú egyenlet.
Tudjuk még, hogy \(\displaystyle \beta=19^\circ,\) vagyis \(\displaystyle \tg\beta=0{,}344.\) Az egyenlet két gyöke:
\(\displaystyle X_1=0{,}56\qquad\textrm{és}\qquad X_2=0{,}89,\)
amelyek a lejtő \(\displaystyle \alpha_1\approx 29^\circ\)-os és \(\displaystyle \alpha_2\approx 42^\circ\)-os hajlásszögének felelnek meg. A feladat feltételeinek ezen szögek bármelyike eleget tesz.
Statistics:
41 students sent a solution. 3 points: Bálint Áron, Beinschroth Máté, Bencze Mátyás, Bense Tamás, Blaskovics Ádám, Bús László Teodor, Éliás Kristóf , Fekete Lúcia, Fercsák Flórián, Illés Dóra, Kis Boglárka 08, Klement Tamás, Konkoly Zoltán, Magyar Zsófia, Misik Balázs, Molnár Lili, Papp Emese Petra, Sütő Áron, Szabó Donát, Szécsi Bence, Tóth Hanga Katalin, Tóth-Tűri Bence, Ujvári Sarolta, Vértesi Janka, Vincze Anna. 2 points: Csipkó Hanga Zoé , Sipos Márton, Varga 511 Vivien, Zámbó Luca. 1 point: 3 students. 0 point: 4 students.
Problems in Physics of KöMaL, December 2024
