 Problem P. 5611. (December 2024)
Problem P. 5611. (December 2024)
P. 5611. The ``double yo-yo'' shown in the figure consists of two identical discs with uniform mass distribution and the yarns wound on them.
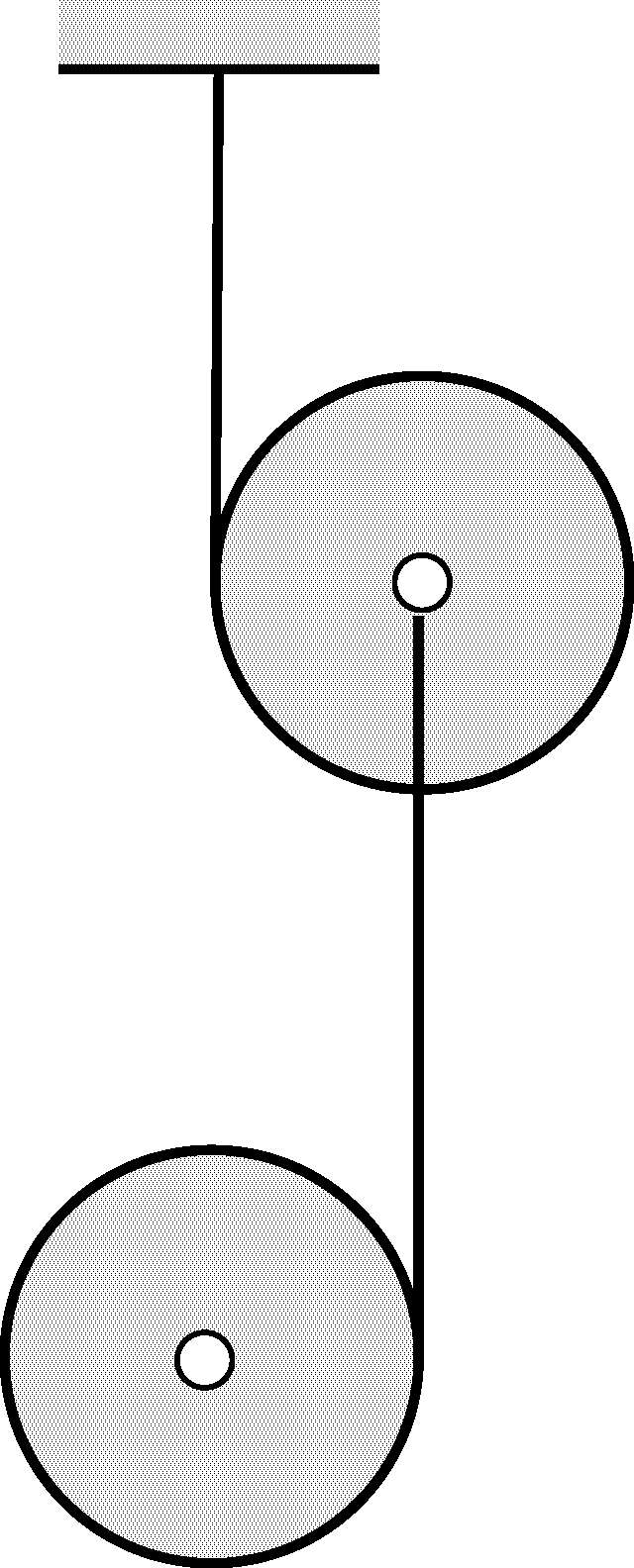
The two discs are released with zero initial velocity such that the yarns are vertical.
a) Which of the two discs' axis will have a greater speed after a certain time elapsed, and how many times this speed is greater than the speed of the axis of the other disc?
b) Which disc's angular speed will be greater after a certain time elapsed, and by what factor will this angular speed be greater than that of the other disc?
(At the moment in question, the yarns have not yet been unwound from the discs.)
(5 pont)
Deadline expired on January 15, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen a korongok tömege \(\displaystyle m\), sugara \(\displaystyle r\), a felső korong tömegközéppontjának gyorsulása \(\displaystyle a_1\), szöggyorsulása \(\displaystyle \beta_1\), az alsó korongé \(\displaystyle a_2\) és \(\displaystyle \beta_2\). A felső fonalat feszítő erőt jelölje \(\displaystyle K_1\), az alsó fonálban ható erőt pedig \(\displaystyle K_2\) (lásd az ábrát).

A következő mozgásegyenleteket írhatjuk fel:
| \(\displaystyle (1)\) | \(\displaystyle mg+K_2-K_1=ma_1,\) |
| \(\displaystyle (2)\) | \(\displaystyle mg-K_2=ma_2,\) |
| \(\displaystyle (3)\) | \(\displaystyle K_1r=\frac12mr^2\beta_1,\) |
| \(\displaystyle (4)\) | \(\displaystyle K_2r=\frac12mr^2\beta_2.\) |
A fonalak hosszának állandósága miatt fennállnak még az
| \(\displaystyle (5)\) | \(\displaystyle a_1=r\beta_1\) |
és az
| \(\displaystyle (6)\) | \(\displaystyle a_2-a_1=r\beta_2\) |
kényszerfeltételek.
Az (1)-(6) lineáris egyenletrendszer megoldásából kapjuk:
\(\displaystyle a_1=\cfrac{8}{11}g\qquad \text{és}\qquad a_2=\cfrac{10}{11}g,\)
továbbá
\(\displaystyle \beta_1=\frac{8}{11}\,\frac{g}{r}\qquad \text{és}\qquad \beta_2=\frac{2}{11}\,\frac{g}{r}.\)
a) A korongok tömegközéppontja egyenletesen gyorsul, a sebességük tehát egy adott idő múlva a gyorsulásukkal arányos. Eszerint az alsó korong sebessége bármely időpontban nagyobb, mint a felső korongé:
\(\displaystyle \frac{v_2}{v_1}=\frac{a_2}{a_1}=\frac{5}{4}.\)
b) A korongok szöggyorsulása állandó, a szögsebességek tehát egy adott pillanatban a szöggyorsulással arányosak:
\(\displaystyle \frac{\omega_1}{\omega_2}=\frac{\beta_1}{\beta_2}=4,\)
tehát a felső korong szögsebessége lesz nagyobb az indulás utáni időpillanatokban.
Statistics:
25 students sent a solution. 5 points: Beke Márton Csaba, Bélteki Teó, Csiszár András, Erdélyi Dominik, Erős Fanni, Gyenes Károly, Kiss 131 Adorján Timon, Masa Barnabás, Molnár Lili, Nagy Gellért Ákos, Papp Emese Petra, Pázmándi József Áron, Sütő Áron, Szécsi Bence, Tóth Hanga Katalin, Tóthpál-Demeter Márk, Ujpál Bálint, Zólomy Csanád Zsolt. 4 points: Kovács Tamás. 3 points: 3 students. 0 point: 1 student.
Problems in Physics of KöMaL, December 2024
