 Problem P. 5617. (January 2025)
Problem P. 5617. (January 2025)
P. 5617. A small body rests at the bottom of a frictionless slope. The slope has an angle of inclination of \(\displaystyle 30^\circ\) and a height of \(\displaystyle 1~\mathrm{m}\). The slope is moved horizontally with an acceleration of \(\displaystyle 7~\mathrm{m/s^2}\). How long does it take for the body to reach the top of the slope?
(4 pont)
Deadline expired on February 17, 2025.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. A lejtővel együtt gyorsuló vonatkoztatási rendszerben a testre az \(\displaystyle mg\) nehézségi erőn és a lejtő \(\displaystyle F_\mathrm{n}\) nyomóerején kívül \(\displaystyle ma_0\) nagyságú, a lejtő gyorsulásával ellentétes irányú (vízszintes) tehetetlenségi erő is hat (1. ábra), ahol \(\displaystyle a_0=7\,\mathrm{m/s^2}\) a lejtő gyorsulása az inerciarendszerben.

1. ábra
A mozgásegyenletek:
$$\begin{gather*} ma=ma_0\cos\alpha-mg\sin\alpha,\\ F_\mathrm{n}=ma_0\sin\alpha+mg\cos\alpha, \end{gather*}$$hiszen a test – ebben a vonatkoztatási rendszerben – csak a lejtő síkjával párhuzamosan mozoghat. Az első egyenletből:
\(\displaystyle a=a_0\cos\alpha-g\sin\alpha\approx 1{,}16\,\mathrm{m/s^2}.\)
Ebben a vonatkoztatási rendszerben a lejtő áll, és a testnek a lejtőn kell végighaladnia. A \(\displaystyle h\) magasságú lejtő hossza
\(\displaystyle s=\frac{h}{\sin\alpha}=2\,\mathrm{m},\)
az egyenletesen gyorsuló test ezt a távolságot
\(\displaystyle t=\sqrt{\frac{2s}{a}}\approx 1{,}86\,\mathrm{s}\)
idő alatt teszi meg.
Megjegyzés. a test csak akkor indul el felfelé a lejtőn, ha \(\displaystyle a=a_0\cos\alpha-g\sin\alpha>0\), amiből az \(\displaystyle a_0>g\tg\alpha\) feltétel adódik. \(\displaystyle 30^\circ\)-os lejtő esetében ez \(\displaystyle a_0>5{,}66\,\mathrm{m/s^2}\) feltételt jelent.
II. megoldás. A lejtővel együtt gyorsuló vonatkoztatási rendszerben minden testre hat az \(\displaystyle mg\) nehézségi erő és az \(\displaystyle ma_0\) nagyságú tehetetlenségi erő is, így a testek azt ,,érzik'' mintha \(\displaystyle \boldsymbol{g}'=\boldsymbol{g}+\boldsymbol{a}_0\) nehézségi gyorsulás lenne. A \(\displaystyle \boldsymbol{g}'\) nagysága:
\(\displaystyle g'=\sqrt{g^2+a_0^2}\approx 12{,}05\,\mathrm{m/s^2},\)
iránya pedig
\(\displaystyle \gamma=\arctg\frac{a_0}{g}\approx 35{,}5^\circ\)
szöget zár be a függőlegessel (2/a ábra). Ebben az erőtérben a test úgy mozog, mintha egy \(\displaystyle \beta=\gamma-\alpha\approx 5{,}5^\circ\) hajlásszögű lejtőn csúszna le \(\displaystyle g'\) nehézségi gyorsulás mellett (2/b ábra).
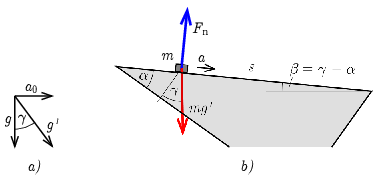
2. ábra
A súrlódásmentes lejtőn lecsúszó test gyorsulása jól ismert:
\(\displaystyle a=g'\sin\beta\approx 1{,}16\,\mathrm{m/s^2},\)
amiből a ,,lecsúszás'' ideje az előző megoldással egyező módon \(\displaystyle t\approx 1{,}86\,\mathrm{s}\).
III. megoldás. A feladat inerciarendszerben is megoldható. Ekkor a testre csak a nehézségi erő és a lejtő nyomóereje hat, azonban a test nem a lejtő síkjában fog mozogni (hiszen ebben a vonatkoztatási rendszerben a lejtő is mozog). Az erőket és az elmozdulásokat a 3. ábra mutatja (az ábra méretei torzítottak).
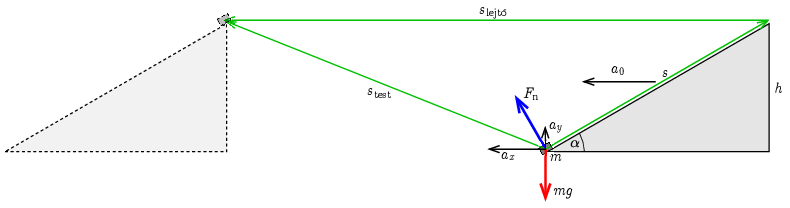
3. ábra
A mozgásegyenletek:
$$\begin{gather*} ma_x=F_\mathrm{n}\sin\alpha,\tag{1}\\ ma_y=F_\mathrm{n}\cos\alpha-mg\tag{2}, \end{gather*}$$ahol \(\displaystyle a_x\) és \(\displaystyle a_y\) a test vízszintes és függőleges gyorsuláskomponense.
Másrészt az ábráról leolvasható, hogy a test és a lejtő elmozdulásvektorának különbsége egyenlő a lejtő aljától a tetejéig mutató vektorral:
\(\displaystyle \boldsymbol{s}_\textrm{test}-\boldsymbol{s}_\textrm{lejtő}=\boldsymbol{s}.\)
A test és a lejtő elmozdulásvektora is arányos a gyorsulásvektorukkal (hiszen ugyanannyi ideig és egyenes vonalban, zérus kezdősebességről egyenletesen gyorsulva mozog mindkettő), így ebből a gyorsulásokra adódó feltétel:
| \(\displaystyle (3)\) | \(\displaystyle \frac{a_y}{a_0-a_x}=\tg\alpha.\) |
Az (1), (2) és (3) egyenletekből álló egyenletrendszert megoldva:
\(\displaystyle a_y=a_0\sin\alpha\cos\alpha-g\sin^2\alpha\approx 0{,}58\,\mathrm{m/s^2}.\)
A testnek \(\displaystyle h=1\,\mathrm{m}\) magasra kell feljutnia, ehhez
\(\displaystyle t=\sqrt{\frac{2h}{a_y}}\approx 1{,}86\,\mathrm{s}\)
időre van szükség.
Megjegyzés. A feladat nem kérdezi, de meghatározhatjuk a lejtő elmozdulását is: a lejtő
\(\displaystyle d=\frac{a_0}{2}t^2=\frac{a_0}{a_y}h=\frac{a_0}{a_0\sin\alpha\cos\alpha-g\sin^2\alpha}h\approx 12{,}1\,\mathrm{m}\)
utat tesz meg (ezért kellett torzított ábrát készíteni).
Statistics:
61 students sent a solution. 4 points: Balázs Barnabás, Bálint Áron, Bélteki Teó, Bencze Mátyás, Bense Tamás, Benyó Júlia , Bús László Teodor, Csipkó Hanga Zoé , Csiszár András, Domján Noémi Dóra, Elekes Panni, Erős Fanni, Fekete Lúcia, Fercsák Flórián, Hajdu Eszter, Hornok Máté, Hübner Júlia, Illés Dóra, Kis Boglárka 08, Konkoly Zoltán, Kovács Tamás, Magyar Zsófia, Masa Barnabás, Molnár Lili, Papp Emese Petra, Sárecz Bence, Sütő Áron, Szabó Donát, Szécsi Bence, Tóthpál-Demeter Márk, Ujpál Bálint, Varga 802 Zsolt, Wolf Erik. 3 points: Blaskovics Ádám, Éliás Kristóf , Magyar Levente Árpád, Pituk Péter, Sipos Márton, Varga Zétény, Vértesi Janka, Vincze Anna, Zólomy Csanád Zsolt. 2 points: 5 students. 1 point: 5 students. 0 point: 3 students.
Problems in Physics of KöMaL, January 2025
