 Problem P. 5626. (February 2025)
Problem P. 5626. (February 2025)
P. 5626. A motorcyclist starts from rest and travels in a circular path such that the speed of the motorcyclist increases uniformly. What is the angle turned (with respect to the initial position) until the direction of the acceleration of the motorcycle first becomes perpendicular to the direction of the initial acceleration?
(5 pont)
Deadline expired on March 17, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A motorosnak kezdetben csak érintőirányú gyorsulása van, később viszont a gyorsulásvektora az \(\displaystyle a_\mathrm{t}\) nagyságú tangenciális és az \(\displaystyle a_\mathrm{cp}\) nagyságú centripetális gyorsulás eredője. Jelöljük a keresett elfordulási szöget \(\displaystyle \alpha\)-val. Az 1. ábrán látható, hogy amikor az eredő gyorsulás először merőleges a kezdeti gyorsulásra, akkor
| \(\displaystyle (1)\) | \(\displaystyle \ctg\alpha=\frac{a_\mathrm{cp}}{a_\mathrm{t}}.\) |
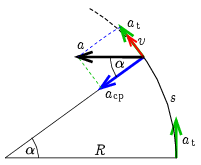
1. ábra
A nulla kezdősebességről állandó \(\displaystyle a_\mathrm{t}\) érintőirányú gyorsulással mozgó testre fennáll:
\(\displaystyle v^2=2a_\mathrm{t}s=2a_\mathrm{t}R\alpha,\)
ahol \(\displaystyle v\) a motoros sebessége az \(\displaystyle s=R\alpha\) út megtétele után. A centripetális gyorsulás:
\(\displaystyle a_\mathrm{cp}=\frac{v^2}{R}=\frac{2a_\mathrm{t}R\alpha}{R}=2a_\mathrm{t}\alpha.\)
Ezt behelyettesítve az (1) kifejezésbe a
\(\displaystyle \ctg\alpha=2\alpha\)
transzcendens egyenletet kapjuk.
Az egyenletet iterálással vagy grafikusan (2. ábra) megoldva a keresett elfordulási szög:
\(\displaystyle \alpha=0{,}653\approx 37^\circ.\)
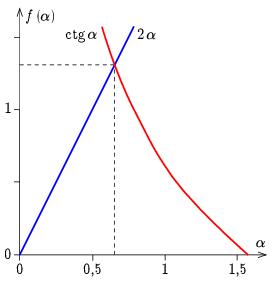
2. ábra
Az iterálásnál egy tetszőleges \(\displaystyle 0<\alpha_0<\tfrac{\pi}{2}\) értékről elindulhatunk. Ezután az
\(\displaystyle \alpha_{i+1}=\frac{\alpha_i+\frac{\ctg\alpha_i}{2}}{2}\)
eljárást addig folytatjuk, amíg az értéket kellő pontossággal megkapjuk. Ha \(\displaystyle \alpha_0=1\) értékről indulunk, akkor négy tizedesre számolva
$$\begin{gather*} \alpha_1=0{,}6605,\\ \alpha_2=0{,}6520,\\ \alpha_3=0{,}6535,\\ \alpha_4=0{,}6532,\\ \alpha_5=0{,}6533,\\ \alpha_6=0{,}6533. \end{gather*}$$Ugyanilyen jó a ,,fordított''
\(\displaystyle \alpha_{i+1}=\frac{\alpha_i+\arcctg(2\alpha_i)}{2}\)
algoritmus. Ekkor, szintén \(\displaystyle \alpha_0=1\)-ről indulva:
$$\begin{gather*} \alpha_1=0{,}7318,\\ \alpha_2=0{,}6656,\\ \alpha_3=0{,}6549,\\ \alpha_4=0{,}6534,\\ \alpha_5=0{,}6533,\\ \alpha_6=0{,}6533. \end{gather*}$$Megjegyzés. Lassabban konvergál, de egy zsebszámológépen* (természetesen radián állásban) például 1 kiinduló értékről indulva periodikusan a
$$\begin{gather*} \times\\ 2\\ =\\ \textrm{1/x}\\ \textrm{INV tan} \end{gather*}$$gombokat nyomkodva (mindaddig, míg kellő pontossággal ugyanaz az érték adódik) szintén megkapjuk az eredményt. (Ugyanakkor a ,,másik irányban'' próbálkozva, a
$$\begin{gather*} \textrm{tan}\\ \textrm{1/x}\\ \div\\ 2\\ = \end{gather*}$$lépéssor divergens lesz.)
*Az eljárás részletei attól függenek, hogy milyen zsebszámológépet használunk. Az itt leírtak egy egyszerű TI-30 SLR számológép jelöléseit tartalmazzák.
Statistics:
39 students sent a solution. 5 points: Bálint Áron, Beke Márton Csaba, Bélteki Teó, Bencze Mátyás, Bense Tamás, Blaskovics Ádám, Csipkó Hanga Zoé , Csiszár András, Elekes Panni, Erdélyi Dominik, Fekete Lúcia, Kis Boglárka 08, Kiss 131 Adorján Timon, Klement Tamás, Kovács Tamás, Misik Balázs, Molnár Lili, Papp Emese Petra, Simon János Dániel, Sütő Áron, Szécsi Bence, Tóth Hanga Katalin, Tóth-Tűri Bence, Ujpál Bálint, Ujvári Sarolta, Vértesi Janka, Zólomy Csanád Zsolt. 3 points: 4 students. 2 points: 2 students. 0 point: 3 students.
Problems in Physics of KöMaL, February 2025
