Problem P. 5635. (March 2025)

P. 5635. A gymnast, performing a giant on a high bar, is just tipping over the vertical position at the top. When he reaches the bottom, the steel bar is visibly bent. Let us model the gymnast with a thin, heavy, uniform beam rotating around a horizontal axis (the steel bar). When the beam reaches the bottom from its top position, by what factor of its weight does it pull the bar? (Neglect friction, air resistance, and bending of the bar with respect to the length of the beam.)

(4 pont)

Deadline expired on April 15, 2025.

Sorry, the solution is available only in Hungarian. Google translation

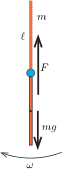
Megoldás. Jelöljük a tornászt modellező rúd tömegét \(\displaystyle m\)-mel, hosszát \(\displaystyle \ell\)-lel. Egy ilyen rúdnak a végpontján átmenő, rá merőleges tengelyre vonatkoztatott tehetetlenségi nyomatéka \(\displaystyle \Theta=\tfrac{1}{3}m\ell^2.\)

Miközben a rúd a felső állásból az alsóba ér, a tömegközéppontja \(\displaystyle \ell\) távolsággal mélyebbre kerül, tehát a helyzeti energiája \(\displaystyle mg\ell\)-lel csökken. Ha a kezdetben álló rúd szögsebessége a legmélyebb helyzetben \(\displaystyle \omega\) lesz, akkor a mozgási energiája \(\displaystyle \frac{1}{2}\Theta\omega^2\)-tel növekszik.

Elhanyagolható súrlódás és közegellenállás esetén alkalmazható a mechanikai energia megmaradásának tétele:

\(\displaystyle mg\ell=\frac{1}{2}\left(\frac{1}{3}m\ell^2\right)\omega^2,\)

vagyis a rúd maximális szögsebessége:

\(\displaystyle \omega=\sqrt{\frac{6g}{\ell}}.\)

A rúd alsó helyzetében a rúd tömegközéppontja

\(\displaystyle v=\frac{1}{2}\ell\omega=\sqrt{\frac{3}{2}g\ell}\)

sebességgel \(\displaystyle \ell/2\) sugarú körpályán mozog, így a gyorsulása függőlegesen felfelé

\(\displaystyle a=\frac{v^2}{\ell/2}=3g.\)

A rúd tömegközéppontjára felírható mozgásegyenlet:

\(\displaystyle F-mg=ma,\)

ahonnan a tengely által kifejtett erő:

\(\displaystyle F=4mg.\)

Ennek az erőnek az ellenereje a nyújtó tengelyére ható, függőlegesen lefelé irányuló, \(\displaystyle 4mg\) nagyságú erő, ez okozza a nyújtó rúdjának lehajlását.

Statistics:

41 students sent a solution.
4 points:	Bélteki Teó, Bencze Mátyás, Bense Tamás, Blaskovics Ádám, Bús László Teodor, Csiszár András, Éliás Kristóf , Fekete Lúcia, Kis Boglárka 08, Misik Balázs, Molnár Lili, Papp Emese Petra, Páternoszter Tamás, Sütő Áron, Tóth-Tűri Bence, Ujpál Bálint, Vértesi Janka, Vincze Anna, Zámbó Luca.
3 points:	Balázs Barnabás, Elekes Panni, Hajdu Eszter, Hornok Máté, Kávai Ádám, Kovács Tamás, Magyar Zsófia, Masa Barnabás, Monok Péter, Nagy Gellért Ákos, Pituk Péter, Sárecz Bence, Szécsi Bence, Tóth Bertalan, Ujvári Sarolta, Varga 802 Zsolt.
2 points:	1 student.
1 point:	2 students.

Problems in Physics of KöMaL, March 2025