 Problem P. 5644. (April 2025)
Problem P. 5644. (April 2025)
P. 5644. With what single mass \(\displaystyle m\) should the pulley with the two masses on the right in the figure be replaced so that the body with mass \(\displaystyle m_1\) moves in the same way as it did originally? Neglect the mass of the pulleys and friction.
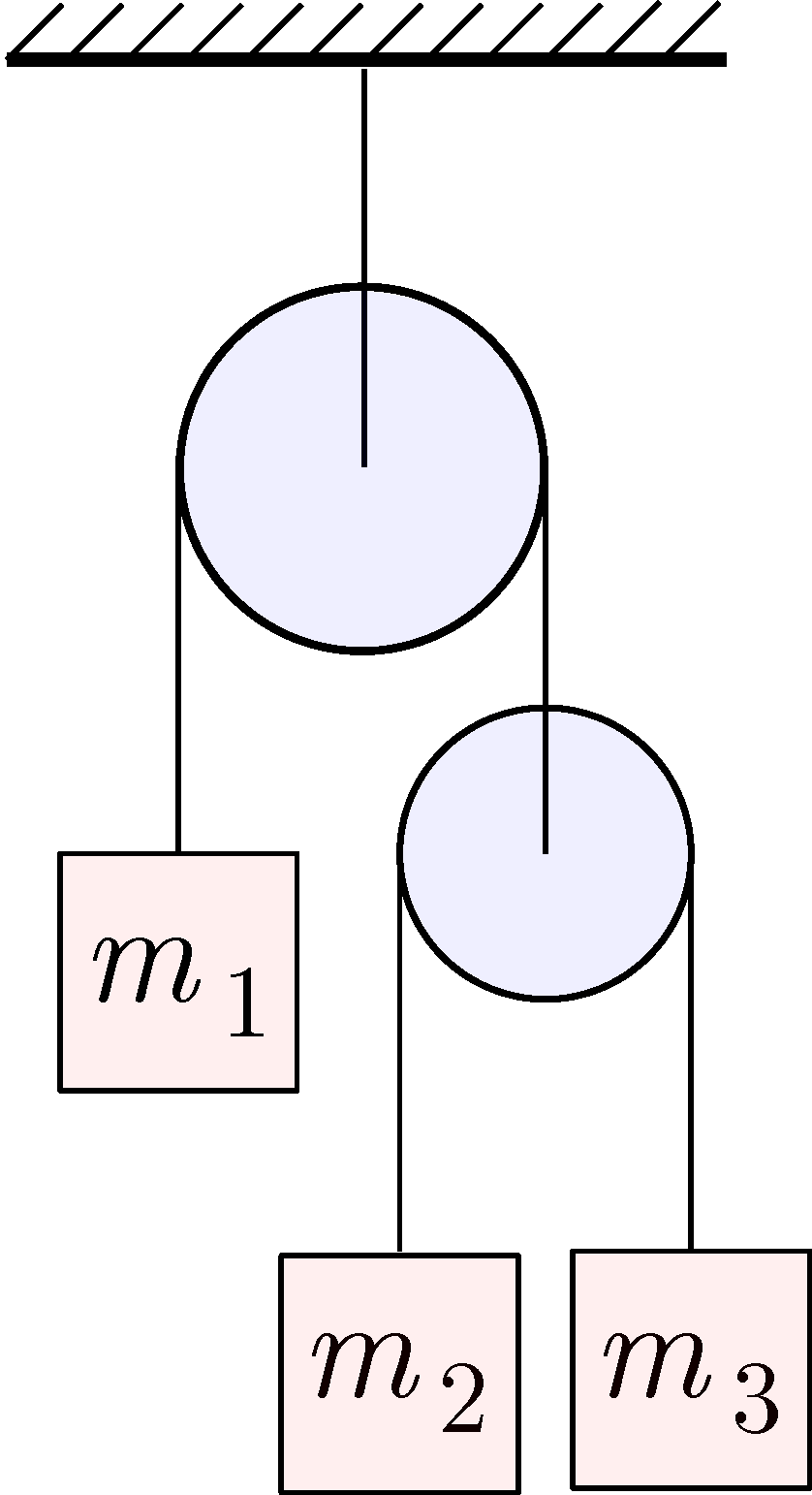
(4 pont)
Deadline expired on May 15, 2025.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Vizsgáljuk a mozgást a jobb oldali csigával együtt mozgó vonatkoztatási rendszerben. A csiga gyorsulása legyen \(\displaystyle a^\star\), és vegyük felfelé pozitívnak (értéke az adatoktól függően pozitív, negatív vagy zérus is lehet). Ebben a rendszerben vizsgálva a mozgást az \(\displaystyle m_i\) tömegű testre az \(\displaystyle m_ig\) nehézségi erőn kívül egy \(\displaystyle m_ia^\star\) nagyságú, lefelé mutató tehetetlenségi erő hatását is figyelembe kell vennünk, tehát olyan, mintha a nehézségi gyorsulás értéke \(\displaystyle g^\star=g+a^\star\) lenne.

1. ábra
Az 1. ábra alapján a mozgásegyenletek (\(\displaystyle m_2\geq m_3\) feltételezéssel, de ennek az indexek felcserélhetősége miatt nincs jelentősége):
$$\begin{gather*} m_2a=m_2g^\star-K,\\ m_3a=K-m_3g^\star. \end{gather*}$$Ebből
\(\displaystyle a=\frac{m_2-m_3}{m_2+m_3}g^\star\qquad\textrm{és}\qquad K=\frac{2m_2m_3}{m_2+m_3}g^\star.\)
A csigát tartó kötélre (a csiga elhanyagolható tömege miatt) \(\displaystyle 2K\) erő hat. Ha a csigát és a két rajta lógó testet egyetlen \(\displaystyle m\) tömeggel helyettesítenénk, akkor arra – mivel ebben a rendszerben nyugalomban van – \(\displaystyle mg^\star\) erő hatna. Tehát a keresett tömeg:
\(\displaystyle m=\frac{2K}{g^\star}=\frac{4m_2m_3}{m_2+m_3}.\)
II. megoldás.
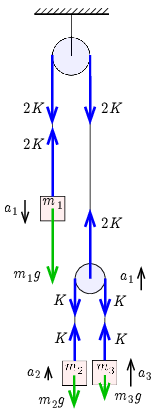
2. ábra
Inerciarendszerben az egész rendszert vizsgáljuk. A 2. ábra alapján a mozgásegyenletek és a kényszerfeltétel:
$$\begin{gather*} m_1a_1=m_1g-2K,\\ m_2a_2=K-m_2g,\\ m_3a_3=K-m_3g,\\ a_3-a_1=a_1-a_2. \end{gather*}$$A lineáris egyenletrendszer megoldása (\(\displaystyle a_2\) és \(\displaystyle a_3\) kifejezésére nem lesz szükségünk, azt csak a teljesség kedvéért írjuk fel):
$$\begin{gather*} a_1=\frac{m_1(m_2+m_3)-4m_2m_3}{m_1(m_2+m_3)+4m_2m_3}g,\\ a_2=\frac{4m_3(m_1-m_2)-m_1(m_2+m_3)}{m_1(m_2+m_3)+4m_2m_3}g,\\ a_3=\frac{4m_2(m_1-m_3)-m_1(m_2+m_3)}{m_1(m_2+m_3)+4m_2m_3}g,\\ K=\frac{4m_1m_2m_3g}{m_1(m_2+m_3)+4m_2m_3}. \end{gather*}$$Ha a jobb oldali csiga és a rajta lógó tömegek helyett egyetlen tömeg lenne, akkor annak a mozgásegyenlete így nézne ki:
\(\displaystyle ma_1=2K-mg.\)
Ebből a keresett tömeg \(\displaystyle K\) és \(\displaystyle a_1\) behelyettesítésével:
\(\displaystyle m=\frac{2K}{a_1+g}=\frac{\frac{8m_1m_2m_3g}{m_1(m_2+m_3)+4m_2m_3}}{\left(\frac{m_1(m_2+m_3)-4m_2m_3}{m_1(m_2+m_3)+4m_2m_3}+1\right)g}=\frac{\frac{8m_1m_2m_3g}{m_1(m_2+m_3)+4m_2m_3}}{\frac{2m_1(m_2+m_3)g}{m_1(m_2+m_3)+4m_2m_3}}=\frac{4m_2m_3}{m_2+m_3},\)
az első megoldással megegyezően.
Megjegyzés. Észrevehetjük, hogy a végeredmény nem függ \(\displaystyle m_1\)-től. Így inerciarendszerben is megoldhatjuk a feladatot az I. megoldáshoz hasonlóan: \(\displaystyle a_1\) értékét ne akarjuk meghatározni (,,bízva'' abban, hogy úgyis kiesik a végeredményből), hanem vegyük fel paraméternek. Ekkor a két jobb oldali test mozgásegyenlete és a kényszerfeltétel a 2. ábra alapján:
$$\begin{gather*} m_2a_2=K-m_2g,\\ m_3a_3=K-m_3g,\\ a_3-a_1=a_1-a_2. \end{gather*}$$Ebből
\(\displaystyle K=\frac{2m_2m_3(a_1+g)}{m_2+m_3},\)
és
\(\displaystyle m=\frac{2K}{a_1+g}=\frac{4m_2m_3}{m_2+m_3}\)
azonnal adódik.
Persze ez ,,bújtatva'' az I. megoldás, hiszen \(\displaystyle a_1\) éppen \(\displaystyle a^\star\)-gal, és így \(\displaystyle a_1+g\) pedig \(\displaystyle g^\star\)-gal egyezik meg.
Statistics:
24 students sent a solution. 4 points: Bencze Mátyás, Csipkó Hanga Zoé , Csiszár András, Molnár Lili, Papp Emese Petra, Szécsi Bence, Vértesi Janka, Zádori Gellért. 3 points: Bélteki Teó, Fekete Lúcia, Konkoly Zoltán. 2 points: 6 students. 1 point: 2 students. 0 point: 3 students.
Problems in Physics of KöMaL, April 2025
