Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem S. 108. (May 2016)

S. 108. Andrew and Brian play a certain game on a tree graph having \(\displaystyle N\) (\(\displaystyle 1\le N\le 100\,000\)) vertices. The game consists of \(\displaystyle M\) (\(\displaystyle 1\le M\le 100\,000\)) steps. Each step is one of the following two possibilities.

– Andrew selects two vertices of the tree, and puts one chocolate on every edge of the unique path between the vertices.

– Brian asks for the number of chocolates on a given edge.

The goal is to answer Brian's questions as quickly as possible.

Your program should read the values of \(\displaystyle N\) and \(\displaystyle M\) from the first line of the standard input, then the tree edges (represented by the integers \(\displaystyle u\) and \(\displaystyle v\)) from the following \(\displaystyle N-1\) lines. Then each of the following \(\displaystyle M\) lines starts with either a letter P or Q, followed by a pair of integers \(\displaystyle u, v\). This last pair denotes a pair of vertices. Letter ``P'' means that Andrew has put one chocolate on every edge of the unique path between the vertices \(\displaystyle (u, v)\). Letter ``Q'' means that Brian has asked for the number of chocolates on the edge \(\displaystyle (u, v)\). Your program should write the answer to Brian's questions in the successive lines of the standard output.

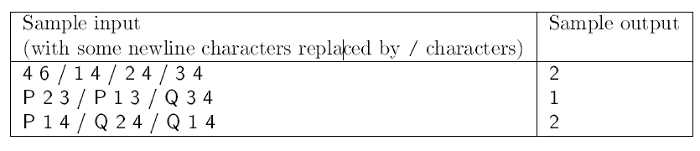
Scoring and bounds. You can get 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any valid input within 1 second of running time.

The source code of your program with a short documentation—also describing which developer environment to use for compiling the source—should be submitted in a compressed file s108.zip.

(10 pont)

Deadline expired on June 10, 2016.

Statistics:

8 students sent a solution.
10 points:Gáspár Attila.
9 points:Janzer Orsolya Lili, Németh 123 Balázs, Noszály Áron.
8 points:2 students.
3 points:1 student.
1 point:1 student.

Problems in Information Technology of KöMaL, May 2016