Az S. 133. feladat (2019. március)

S. 133. Adott $\displaystyle N$ darab természetes szám. $\displaystyle Q$ kérdést/feladatot fogunk adni a számokhoz kapcsolódóan. Egy feladatban vagy minden számot megnövelünk $\displaystyle x$-szel az $\displaystyle [a,b]$ intervallumba eső számaink közül, vagy megkérdezzük, hogy hány szám ad $\displaystyle M$-mel osztva $\displaystyle x$-et maradékul az $\displaystyle [a,b]$ intervallumba eső számaink közül. Készítsünk programot, amely válaszol a kérdésekre.

Bemenet: az első sor tartalmazza az $\displaystyle N$, $\displaystyle M$, $\displaystyle Q$ számokat. A következő sorban az $\displaystyle N$ darab természetes szám található. A következő $\displaystyle Q$ sor mindegyike egy $\displaystyle p\ x\ a\ b$ számnégyest tartalmaz. Ha $\displaystyle p=1$, akkor megkérdezzük, hogy az $\displaystyle [a,b]$ intervallumba eső számaink között hány ad $\displaystyle M$-mel osztva $\displaystyle x$-et maradékul. Ha $\displaystyle p=2$, akkor az összes $\displaystyle [a,b]$ intervallumba eső számunkat megnöveljük $\displaystyle x$-szel.

Kimenet: adjuk meg minden kérdésre a választ, ahol $\displaystyle p=1$. A válaszokat szóközzel választjuk el, a kimenetet egy sorvége jel zárja.

Példa:

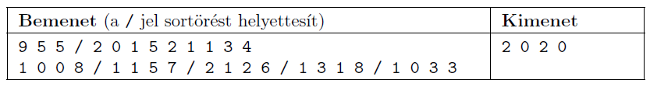
Korlátok: $\displaystyle 1\le N\le 1000$, $\displaystyle 2\le M\le 1000$, $\displaystyle 0<Q\le {10}^{5}$, $\displaystyle 0\le x\le 1000$, $\displaystyle 0\le a\le b\le N-1$. Időlimit: 0,5 mp.

Értékelés: A pontok 20%-a kapható, ha $\displaystyle Q\le 1000$; további 20% kapható, ha $\displaystyle M=2$; további 60% kapható az eredeti korlátokra.

(10 pont)

A beküldési határidő 2019. április 10-én LEJÁRT.

Statisztika:

3 dolgozat érkezett.
10 pontot kapott:	Noszály Áron.
3 pontot kapott:	2 versenyző.

A KöMaL 2019. márciusi informatika feladatai