Az S. 145. feladat (2020. szeptember)

S. 145. Van egy szótárunk \(\displaystyle N\) db szóval. Azt szeretnénk tudni, hányféleképpen tudjuk a szótárból választott szavakat a dominóhoz hasonlóan összeilleszteni úgy, hogy azok \(\displaystyle K\) betű hosszan átfedjék egymást. Tehát a kérdés: hány olyan \(\displaystyle (i,j)\) rendezett számpár (\(\displaystyle 1\le i,j\le N\)) van, melyre az \(\displaystyle i\)-edik szó utolsó \(\displaystyle K\) betűjéből alkotott sorozat megegyezik a \(\displaystyle j\)-edik szó első \(\displaystyle K\) betűjéből alkotott sorozattal.

Bemenet: az első sor tartalmazza az \(\displaystyle N\) és \(\displaystyle K\) számokat. A következő \(\displaystyle N\) sor mindegyike egy, az angol ABC kisbetűiből álló (nem feltétlenül értelmes) szót tartalmaz.

Kimenet: a megfelelő összeillesztések, vagyis számpárok száma.

Példa:

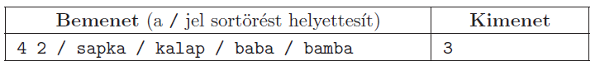
Korlátok: \(\displaystyle 2\le N\le {10}^{5}\), \(\displaystyle 1\le K\le 100\), minden szó legalább \(\displaystyle K\) és legfeljebb 100 betű hosszú. Időkorlát: 1 mp.

Értékelés: a pontok 30%-a kapható \(\displaystyle K=1\) esetén. A pontok további 30%-a kapható, ha \(\displaystyle N\le 100\).

Beküldendő egy s145.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

A beküldési határidő 2020. október 15-én LEJÁRT.

Horcsin Bálint megoldása:

Tároljuk egy \(\displaystyle map\)-ben vagy \(\displaystyle unordered\_map\)-ben azt, hogy egy adott szöveg hány \(\displaystyle elol_i\) -vel egyezik meg. És tároljuk minden \(\displaystyle i\)-re, hogy \(\displaystyle elol_i\overset{?}{=}hatul_i\).
Ezt követően nézzük végig az összes \(\displaystyle i\)-re, hogy \(\displaystyle hatul_i\) hány \(\displaystyle elol_j\)-vel egyezik meg, és ezek összegezzük, és vonjuk le azokat az eseteket, amire \(\displaystyle elol_i=hatul_i\).
Ha \(\displaystyle map\)-et használunk, akkor a futásidő: \(\displaystyle \mathcal{O}(N*logN*K)\)

Megjegyzés:

A feladat úgy is megoldható, hogy a szavak első és utolsó \(\displaystyle K\) karaktereiből két rendezett listát készítünk és ezeket párhuzamosan végignézzük. Ehhez így nem is kell fejlett adatszerkezet.

Statisztika:

18 dolgozat érkezett.
10 pontot kapott:	Bertalan Dániel László, Horcsin Bálint, Németh Márton, Orosz Réka Ildikó, Szakács Ábel, Tóth 211 Bence, Varga 256 Péter.
9 pontot kapott:	Szin Attila.
8 pontot kapott:	1 versenyző.
6 pontot kapott:	1 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2020. szeptemberi informatika feladatai